题目内容
14．
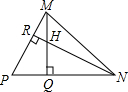已知：如图，在△MPN中，H是高MQ和NR的交点，且MQ=NQ，求证：HN=PM．
分析 先证出∠HNQ=∠PMQ，再由ASA证明△HQN≌△PQM，得出对应边相等即可．
解答 证明：∵H是高MQ和NR的交点，
∴∠PQM=∠HQN=∠PRN=90°，
∴∠P+∠PMQ=90°，∠P+∠HNQ=90°，
∴∠HNQ=∠PMQ，
在△HQN和△PQM中，
$\left\{\begin{array}{l}{∠HQN=∠PQM}&{\;}\\{NQ=MQ}&{\;}\\{∠HNQ=∠PMQ}&{\;}\end{array}\right.$，
∴△HQN≌△PQM（ASA），
∴HN=PM．
点评 本题考查了全等三角形的判定与性质、互余两角的关系；熟练掌握全等三角形的判定与性质是解决问题的关键．
练习册系列答案
相关题目
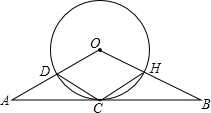如图，等腰三角形AOB的一边BC经过⊙O上的一点C，AO=BO，CA=CB，OA与⊙O交于点D，OB与⊙O交于点H，连接CD、CH．
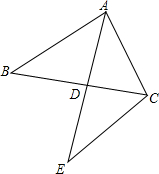已知AD为△ABC中BC边上的中线，CE∥AB交AD的延长线于E．
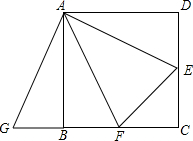已知：如图，在正方形ABCD中，AD=AB，∠D=∠ABC=90°，∠BAD=90°，E，F分别CD，BC边上的点，且∠EAF=45°，延长CB到点G，使BG=DE，连接EF，AG．求证：
