题目内容
9.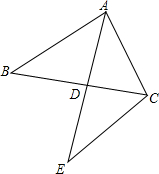 已知AD为△ABC中BC边上的中线,CE∥AB交AD的延长线于E.
已知AD为△ABC中BC边上的中线,CE∥AB交AD的延长线于E.(1)AB=CE吗?为什么?
(2)AD<$\frac{1}{2}$(AB+AC)吗?为什么?
分析 (1)通过全等三角形的判定定理AAS证得△ABD≌△ECD,则该全等三角形的对应边相等,即AB=CE;
(2)由(1)知:△ABD≌△ECD得AB=CE,AD=DE,根据三角形的边角关系得到结论.
解答 解:(1)相等.
证明:∵AD为BC的中线,
∴BD=CD.
∵CE∥AB,
∴∠BAD=∠CED.
在△ABD与△ECD中,
$\left\{\begin{array}{l}{∠BAD=∠CED}\\{∠ADB=∠EDC}\\{BD=CD}\end{array}\right.$,
∴△ABD≌△ECD(AAS),
∴AB=CE;
(2)AD<$\frac{1}{2}$(AB+AC),
证明:由(1)知:△ABD≌△ECD
∴AB=CE,AD=DE,
∵在△ACE中,
AE<CE+AC,
即2AD<AB+AC,
∴AD<$\frac{1}{2}$(AB+AC).
点评 本题考查了全等三角形的判定与性质.三角形的边角关系,在应用全等三角形的判定时,要注意三角形间的公共边、对顶角以及公共角,必要时添加适当辅助线构造三角形.

练习册系列答案
相关题目
19.已知$\frac{a}{b}$=$\frac{3}{4}$,则$\frac{a+b}{b}$=( )
| A. | $\frac{1}{4}$ | B. | $\frac{3}{4}$ | C. | $\frac{7}{4}$ | D. | $\frac{4}{7}$ |
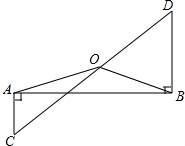 如图:AC⊥AB,DB⊥AB,OC=OD.求证:OA=OB.
如图:AC⊥AB,DB⊥AB,OC=OD.求证:OA=OB.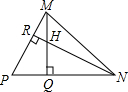 已知:如图,在△MPN中,H是高MQ和NR的交点,且MQ=NQ,求证:HN=PM.
已知:如图,在△MPN中,H是高MQ和NR的交点,且MQ=NQ,求证:HN=PM.
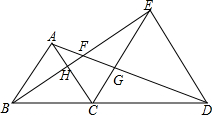 已知等边△ABC,等边△CDE,B、C、D共线.
已知等边△ABC,等边△CDE,B、C、D共线.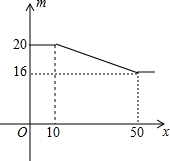 我市一家电子计算器专卖店的某种计算机每个进价13元,零售价20元,多买优惠;若顾客一次购买的数量x(个)与售出的单价m(元/个)的关系如图所示,售出的最低价为每个16元
我市一家电子计算器专卖店的某种计算机每个进价13元,零售价20元,多买优惠;若顾客一次购买的数量x(个)与售出的单价m(元/个)的关系如图所示,售出的最低价为每个16元