题目内容
19.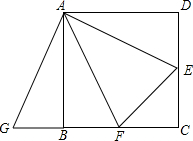 已知:如图,在正方形ABCD中,AD=AB,∠D=∠ABC=90°,∠BAD=90°,E,F分别CD,BC边上的点,且∠EAF=45°,延长CB到点G,使BG=DE,连接EF,AG.求证:
已知:如图,在正方形ABCD中,AD=AB,∠D=∠ABC=90°,∠BAD=90°,E,F分别CD,BC边上的点,且∠EAF=45°,延长CB到点G,使BG=DE,连接EF,AG.求证:(1)△ADE≌△ABG;
(2)EF=DE+BF.
分析 (1)由SAS即可证明△ADE≌△ABG;
(2)由△ADE≌△ABG得出AE=AG,∠DAE=∠BAG,再证出∠GAF=45°,证明△AEF≌△AGF,得出EF=GF,即可得出结论.
解答 证明:(1)∵∠ABC=90°,
∴∠ABG=90°,
在△ADE和△ABG中,
$\left\{\begin{array}{l}{AD=AB}&{\;}\\{∠D=∠ABG=90°}&{\;}\\{DE=BG}&{\;}\end{array}\right.$,
∴△ADE≌△ABG(SAS);
(2)∵△ADE≌△ABG,
∴AE=AG,∠DAE=∠BAG,
∵∠BAD=90°,∠EAF=45°,
∴∠BAF+∠DAE=45°,
∴BAF+∠BAG=45°,
即∠GAF=45°,
∴∠EAF=∠GAF,
在△AEF和△AGF中,
$\left\{\begin{array}{l}{AE=AG}&{\;}\\{∠EAF=∠GAF}&{\;}\\{AF=AF}&{\;}\end{array}\right.$,
∴△AEF≌△AGF(SAS),
∴EF=GF,
∵GF=BG+BF=DE+BF,
∴EF=DE+BF.
点评 本题考查了正方形的性质、全等三角形的判定与性质;熟练掌握正方形的性质,证明三角形全等是解决问题的关键.

练习册系列答案
相关题目
10.下列分解因式正确的是( )
| A. | x3-x=x(x2-1) | B. | x2+y2=(x+y)(x-y) | C. | (a+4)(a-4)=a2-16 | D. | m2+m+$\frac{1}{4}$=(m+$\frac{1}{2}$)2 |
8.三角形的高线是( )
| A. | 直线 | B. | 线段 | C. | 射线 | D. | 三种情况都有 |
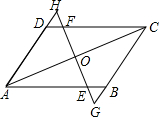 如图,已知AD∥BC,AD=BC,O为AC的中点,过点O作直线交AB于点E,交DC于F,交AD的延长线于H,交CB的延长线于G.
如图,已知AD∥BC,AD=BC,O为AC的中点,过点O作直线交AB于点E,交DC于F,交AD的延长线于H,交CB的延长线于G.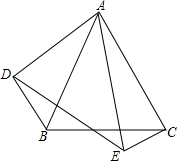 如图,△ABC和△DAE中,∠BAC=∠DAE,AB=AE,AC=AD,连接BD,CE.
如图,△ABC和△DAE中,∠BAC=∠DAE,AB=AE,AC=AD,连接BD,CE.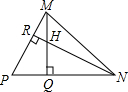 已知:如图,在△MPN中,H是高MQ和NR的交点,且MQ=NQ,求证:HN=PM.
已知:如图,在△MPN中,H是高MQ和NR的交点,且MQ=NQ,求证:HN=PM.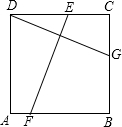 如图,E,F,G是正方形ABCD的边DC,AB,BC上的点,点D与点G关于EF对称,若DG=9cm,则EF=9cm.
如图,E,F,G是正方形ABCD的边DC,AB,BC上的点,点D与点G关于EF对称,若DG=9cm,则EF=9cm.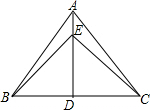 如图,AD是△ABC的高.在AD上取点E,使DE=BD,CE=AB,连接BE
如图,AD是△ABC的高.在AD上取点E,使DE=BD,CE=AB,连接BE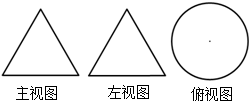 如图是某个几何体的三视图,该几何体是圆锥.
如图是某个几何体的三视图,该几何体是圆锥.