题目内容
3.(1)问题探究:如图①,四边形ABCD,DEFG都是正方形,连接AE,CG,观察图形,猜想AE与CG之间的数量关系和位置关系,并说明你的猜想.
(2)拓展延伸:
如图②,若将“问题探究”中的正方形改为正三角形,试确定AE与BD之间的数量关系,并求出∠APB的度数.

分析 (1)由四边形ABCD和四边形DEFG都是正方形,易证得△ADE≌△CDG,然后由全等三角形的性质,即可证得AE=CG,AE⊥CG.
(2)易证△DCB≌△ECA,得到AE=BD,根据三角形内角和易得∠APB=60°.
解答 解:(1)AE=CG,AE⊥CG.理由:
如图1,∵四边形ABCD和四边形DEFG都是正方形,
∴AD=CD,ED=GD,∠ADC=∠EDG=90°,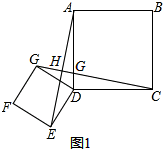
∴∠ADE=∠CDG,
在△ADE和△CDG中,
$\left\{\begin{array}{l}{AD=CD}\\{∠ADE=∠CDG}\\{ED=GD}\end{array}\right.$,
∴△ADE≌△CDG(SAS),
∴AE=CG,∠EAD=∠GCD,
∵∠AGH=∠CGD,
∴∠AHG=∠CDG=90°,
∴AE⊥CG;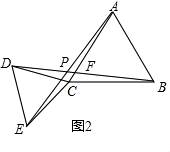
(2)AE=BD,∠APB=60°,
易证△DCB≌△ECA,
∴AE=BD,∠AEC=∠BDC,
∵∠PED+∠PEC=60°,
∴∠PED+∠BDC=60°,
∵∠EDC=60°,
∴∠APB=60°.
点评 此题考查了正方形的性质、等边三角形的性质、全等三角形的判定与性质以及垂直的定义.此题难度适中,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
13.下列事件中是随机事件的是( )
| A. | 测量某天的最低气温,结果是-150℃ | |
| B. | 三角形内角和等于180° | |
| C. | 随意翻一本书的页码,这页的页码是奇数 | |
| D. | 通常加热到100℃时,水沸腾 |
8.三角形的高线是( )
| A. | 直线 | B. | 线段 | C. | 射线 | D. | 三种情况都有 |
12.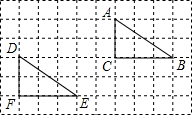 如图,在10×6的网格中,每个小方格的边长都是1个单位,将△DEF平移到△ABC的位置,下列平移方法正确的是( )
如图,在10×6的网格中,每个小方格的边长都是1个单位,将△DEF平移到△ABC的位置,下列平移方法正确的是( )
 如图,在10×6的网格中,每个小方格的边长都是1个单位,将△DEF平移到△ABC的位置,下列平移方法正确的是( )
如图,在10×6的网格中,每个小方格的边长都是1个单位,将△DEF平移到△ABC的位置,下列平移方法正确的是( )| A. | 先向左平移5个单位,再向下平移2个单位 | |
| B. | 先向右平移5个单位,再向下平移2个单位 | |
| C. | 先向左平移5个单位,再向上平移2个单位 | |
| D. | 先向右平移5个单位,再向上平移2个单位 |
13.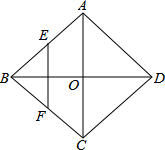 如图,菱形ABCD的对角线AC,BD相交于O点,E,F分别是AB,BC边上的中点,连接EF.若EF=$\sqrt{3}$,BD=4,则菱形ABCD的周长为( )
如图,菱形ABCD的对角线AC,BD相交于O点,E,F分别是AB,BC边上的中点,连接EF.若EF=$\sqrt{3}$,BD=4,则菱形ABCD的周长为( )
 如图,菱形ABCD的对角线AC,BD相交于O点,E,F分别是AB,BC边上的中点,连接EF.若EF=$\sqrt{3}$,BD=4,则菱形ABCD的周长为( )
如图,菱形ABCD的对角线AC,BD相交于O点,E,F分别是AB,BC边上的中点,连接EF.若EF=$\sqrt{3}$,BD=4,则菱形ABCD的周长为( )| A. | 4 | B. | 4$\sqrt{6}$ | C. | 4$\sqrt{7}$ | D. | 28 |
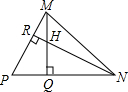 已知:如图,在△MPN中,H是高MQ和NR的交点,且MQ=NQ,求证:HN=PM.
已知:如图,在△MPN中,H是高MQ和NR的交点,且MQ=NQ,求证:HN=PM.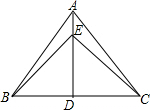 如图,AD是△ABC的高.在AD上取点E,使DE=BD,CE=AB,连接BE
如图,AD是△ABC的高.在AD上取点E,使DE=BD,CE=AB,连接BE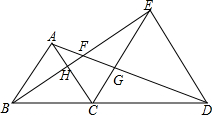 已知等边△ABC,等边△CDE,B、C、D共线.
已知等边△ABC,等边△CDE,B、C、D共线.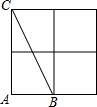 如图,△ABC的3个顶点分别在小正方形的顶点(格点)上,这样的三角形叫格点三角形,该图中与△ABC全等的不同格点三角形共有15个(△ABC除外).
如图,△ABC的3个顶点分别在小正方形的顶点(格点)上,这样的三角形叫格点三角形,该图中与△ABC全等的不同格点三角形共有15个(△ABC除外).