��Ŀ����
2������֪�����������������ȫ�ȣ������������ȣ���������ȫ�ȵ������Σ���ijЩ����£���ͨ��֤���ȵȸ���˵�����ǵ������ȣ���֪��ABC���DEC�ǵ���ֱ�������Σ���ACB=��DCE=90�㣬����AD��BE��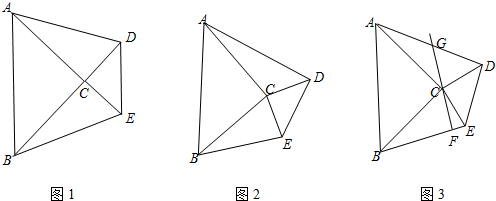
��1����ͼ1������BCE=90��ʱ����֤��S��ACD=S��BCE��
��2����ͼ2����0�㣼��BCE��90��ʱ�����������Ƿ���Ȼ�����������������֤���������������˵�����ɣ�
��3����ͼ3���ڣ�2���Ļ����ϣ���CF��BE���ӳ�FC��AD�ڵ�G����֤����GΪAD�е㣮
���� ��1�����ݡ�ABC���DEC�ǵ���ֱ�������Σ��õ�AC=BC��DC=EC����ACB=��DCE�ɡ�BCE=90�㣬֤�á�ACE=��BCE���Ƴ���ACD�ա�BCE���Ӷ�֤�ý���S��ACE=S��BCE��
��2����AG��ֱDC���ӳ����ڵ�G����BH��CE������ΪH�����ڡ�ACB=��GCE=90�㣬�õ���ACG=��BCH���Ƴ���ACG�ա�BCH���ó�AG=BH������CD=CE�����ǵõ������S��ACE=S��BCE��
��3����AM��ֱCG���ӳ����ڵ�M����DN��CG������ΪN��֤�á�ACM�ա�CBF���õ�AM=CF��ͬ����֤��DCN�ա�CEF���õ�DN=CF��AM=DN���Ƴ���AMG�ա�DNG���õ�AG=DG����GΪAD�е㣮
��� ֤������1���ߡ�ABC���DEC�ǵ���ֱ�������Σ�
��AC=BC��DC=EC����ACB=��DCE
�ߡ�BCE=90�㣬
���ACE=��BCE��
�ڡ�ACD���BCE�У�
$\left\{\begin{array}{l}{AC=BC}\\{��ACE=��BCE}\\{DC=EC}\end{array}\right.$��
���ACD�ա�BCE��SAS����
��S��ACE=S��BCE��
��2����AG��ֱDC���ӳ����ڵ�G����BH��CE������ΪH��
�ߡ�ACB=��GCE=90�㣬
���ACG=��BCH��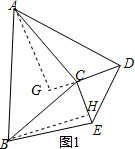
�ڡ�ACG���BCF�У�
$\left\{\begin{array}{l}{��AGC=��BHC}\\{��ACG=��BCH}\\{AC=BC}\end{array}\right.$��
���ACG�ա�BCH��AAS��
��AG=BH
��CD=CE
��$\frac{1}{2}$CD•AG=$\frac{1}{2}$CE•BH��
��S��ACD=S��BCE��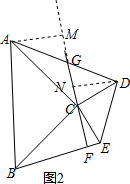
��3����AM��ֱCG���ӳ����ڵ�M����DN��CG������ΪN��
���ACB=90����BFC=90�㣬
���ACM+��BCF=90�㣬��BCF+��CBF=90�㣬
���ACM=��CBF��
�ڡ�ACM���BCF�У�
$\left\{\begin{array}{l}{��AMC=��CFB}\\{��ACM=��CBF}\\{AC=CB}\end{array}\right.$��
���ACM�ա�CBF��AAS����
��AM=CF��
ͬ����֤��DCN�ա�CEF��
��DN=CF��
��AM=DN��
�֡ߡ�AMG=��DNG��
���AGM=��DGN��
�ڡ�AMG���DNG�У�
$\left\{\begin{array}{l}{��AMG=��DNG}\\{��AGM=��DNG}\\{AM=DN}\end{array}\right.$��
���AMG�ա�DNG��AAS����
��AG=DG��
��GΪAD�е㣬
���� ���⿼����ȫ�������ε��ж������ʣ�����ֱ�������ε����ʣ������ε������ʽ����ȷ�������������ǽ���Ĺؼ���

 Сѧ������ҵϵ�д�
Сѧ������ҵϵ�д� ��ʿһ��ȫͨϵ�д�
��ʿһ��ȫͨϵ�д�| A�� | $\left\{\begin{array}{l}{a=1}\\{b=2}\end{array}\right.$ | B�� | $\left\{\begin{array}{l}{a=-4}\\{b=-6}\end{array}\right.$ | C�� | $\left\{\begin{array}{l}{a=-6}\\{b=2}\end{array}\right.$ | D�� | $\left\{\begin{array}{l}{a=14}\\{b=2}\end{array}\right.$ |
| A�� | ����ij���������£������-150�� | |
| B�� | �������ڽǺ͵���180�� | |
| C�� | ���ⷭһ�����ҳ�룬��ҳ��ҳ�������� | |
| D�� | ͨ�����ȵ�100��ʱ��ˮ���� |
| A�� | x3-x=x��x2-1�� | B�� | x2+y2=��x+y����x-y�� | C�� | ��a+4����a-4��=a2-16 | D�� | m2+m+$\frac{1}{4}$=��m+$\frac{1}{2}$��2 |
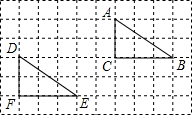 ��ͼ����10��6�������У�ÿ��С����ı߳�����1����λ������DEFƽ�Ƶ���ABC��λ�ã�����ƽ�Ʒ�����ȷ���ǣ�������
��ͼ����10��6�������У�ÿ��С����ı߳�����1����λ������DEFƽ�Ƶ���ABC��λ�ã�����ƽ�Ʒ�����ȷ���ǣ�������| A�� | ������ƽ��5����λ��������ƽ��2����λ | |
| B�� | ������ƽ��5����λ��������ƽ��2����λ | |
| C�� | ������ƽ��5����λ��������ƽ��2����λ | |
| D�� | ������ƽ��5����λ��������ƽ��2����λ |
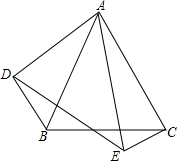 ��ͼ����ABC�͡�DAE�У���BAC=��DAE��AB=AE��AC=AD������BD��CE��
��ͼ����ABC�͡�DAE�У���BAC=��DAE��AB=AE��AC=AD������BD��CE��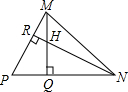 ��֪����ͼ���ڡ�MPN�У�H�Ǹ�MQ��NR�Ľ��㣬��MQ=NQ����֤��HN=PM��
��֪����ͼ���ڡ�MPN�У�H�Ǹ�MQ��NR�Ľ��㣬��MQ=NQ����֤��HN=PM��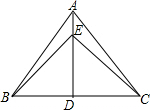 ��ͼ��AD�ǡ�ABC�ĸߣ���AD��ȡ��E��ʹDE=BD��CE=AB������BE
��ͼ��AD�ǡ�ABC�ĸߣ���AD��ȡ��E��ʹDE=BD��CE=AB������BE