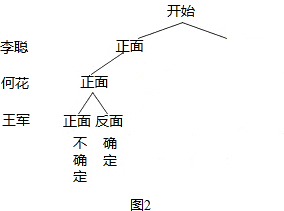
题目内容
2. 已知两点A(-1,1)和B(2,3),要在x轴上找一点P,使AP+BP最小,求点P的坐标.
已知两点A(-1,1)和B(2,3),要在x轴上找一点P,使AP+BP最小,求点P的坐标.
分析 求得B关于x轴的对称点B′的坐标,然后利用待定系数法求得AB′的解析式,然后求得解析式与x轴的交点即可.
解答 解:B关于x轴的对称点B′是(2,-3),
设直线AB′的解析式y=kx+b(k≠0),
将点A(-1,1)、B′(2,-3)的坐标代入得:
$\left\{\begin{array}{l}{-k+b=1}\\{2k+b=-3}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=-\frac{4}{3}}\\{b=-\frac{1}{3}}\end{array}\right.$,
所以直线AB的解析式为:y=-$\frac{4}{3}$x-$\frac{1}{3}$.
令y=0,解得x=-$\frac{1}{4}$,
所以点P的坐标为(-$\frac{1}{4}$,0).
点评 本题考查点的对称以及待定系数法求函数解析式,正确确定P的位置是关键.

练习册系列答案
相关题目
13.某超市一月份的营业额为200万元,三月份的营业额为288万元,如果每月比上一个月增长的百分数相同,则每月的平均增长率为( )
| A. | 10% | B. | 15% | C. | 20% | D. | 25% |
10.在下列实数中,无理数是( )
| A. | 0.010010001 | B. | $\frac{1}{4}$ | C. | $\sqrt{5}$ | D. | 6 |
11.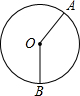 如图,圆中两条半径把圆分成面积为4:5的两个扇形,则两个扇形的圆心角的度数为( )
如图,圆中两条半径把圆分成面积为4:5的两个扇形,则两个扇形的圆心角的度数为( )
 如图,圆中两条半径把圆分成面积为4:5的两个扇形,则两个扇形的圆心角的度数为( )
如图,圆中两条半径把圆分成面积为4:5的两个扇形,则两个扇形的圆心角的度数为( )| A. | 40°和50° | B. | 80°和100° | C. | 120°和150° | D. | 160°和200° |
12.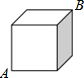 如图,已知正方体的棱长为1,则蚂蚁在表面上从一个顶点A爬行到相对顶点B的最短路程为( )
如图,已知正方体的棱长为1,则蚂蚁在表面上从一个顶点A爬行到相对顶点B的最短路程为( )
 如图,已知正方体的棱长为1,则蚂蚁在表面上从一个顶点A爬行到相对顶点B的最短路程为( )
如图,已知正方体的棱长为1,则蚂蚁在表面上从一个顶点A爬行到相对顶点B的最短路程为( )| A. | 3 | B. | $\sqrt{2}+1$ | C. | $\sqrt{3}$ | D. | $\sqrt{5}$ |
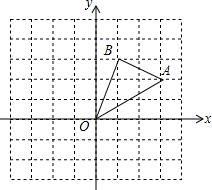 如图,在边长为1的正方形组成的网格中,△AOB的顶点均在格点上,点A,B的坐标分别是A(3,2),B(1,3).△AOB绕点O逆时针旋转90°后得到△A1OB1.
如图,在边长为1的正方形组成的网格中,△AOB的顶点均在格点上,点A,B的坐标分别是A(3,2),B(1,3).△AOB绕点O逆时针旋转90°后得到△A1OB1.