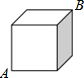如图.已知正方体的棱长为1.则蚂蚁在表面上从一个顶点A爬行到相对顶点B的最短路程为( )A．3B．$\sqrt{2}+1$C．$\sqrt{3}$D．$\sqrt{5}$ 题目和参考答案——青夏教育精英家教网—

题目内容

12．

如图，已知正方体的棱长为1，则蚂蚁在表面上从一个顶点A爬行到相对顶点B的最短路程为（　　）

A．

B．

$\sqrt{2}+1$

C．

$\sqrt{3}$

D．

$\sqrt{5}$

分析先把正方体展开，连接AB，再根据勾股定理求出AB的值即可．

解答解：将正方体展开，如图所示：
在直角△ABC中，∵∠ACB=90°，AC=2，BC=1，
∴AB=$\sqrt{{AC}^{2}+{BC}^{2}}$=$\sqrt{{2}^{2}+{1}^{2}}$=$\sqrt{5}$．
故选D．

点评本题考查的是平面展开-最短路径问题，根据题意把正方体展开，构造出直角三角形，利用勾股定理进行解答即可．

练习册系列答案

相关题目

2．

已知两点A（-1，1）和B（2，3），要在x轴上找一点P，使AP+BP最小，求点P的坐标．

3．观察下列等式$\frac{1}{1×2}=1-\frac{1}{2}$，$\frac{1}{2×3}=\frac{1}{2}-\frac{1}{3}$，$\frac{1}{3×4}=\frac{1}{3}-\frac{1}{4}$，以上三个等式两边分别相加得：$\frac{1}{1×2}+\frac{1}{2×3}+\frac{1}{3×4}=1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}=1-\frac{1}{4}=\frac{3}{4}$
（1）猜想并写出：$\frac{1}{n（n+1）}$=$\frac{1}{n}$-$\frac{1}{n+1}$；
（2）计算：$\frac{1}{1×2}+\frac{1}{2×3}+\frac{1}{3×4}+…+\frac{1}{2006×2007}$=$\frac{2006}{2007}$；
（3）探究并计算：$\frac{1}{2×4}+\frac{1}{4×6}+\frac{1}{6×8}+…+\frac{1}{2006×2008}$=$\frac{1003}{4016}$；
（4）若|ab-3|与|b-1|互为相反数，求：$\frac{1}{ab}$+$\frac{1}{{（{a+2}）（{b+2}）}}$+$\frac{1}{（a+4）（b+4）}$+$\frac{1}{（a+6）（b+6）}$…+$\frac{1}{（a+2016）（b+2016）}$的值．

20．$\frac{13}{7}$，$-3.\stackrel{•}3\stackrel{•}0\stackrel{•}3$，$\sqrt{8}$，$\root{3}{8}$无理数有$\sqrt{8}$．

7．

如图，在△ABC中，AB=AC，点D在AC上，且BD=BC=AD，则∠DBC的度数是（　　）

17．

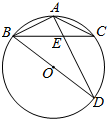如图，BD为⊙O的直径，AB=AC，AD交BC于点E，AE=2，ED=4．
（1）判断△ABE与△ADB是否相似，并说明理由；
（2）求AB的长；
（3）求∠C的正切值．

4．

如图，一个直角三角形纸片，剪去直角后，得到一个四边形，则∠1+∠2=（　　）

1．

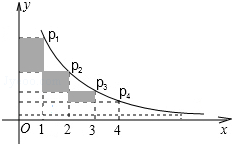如图，在反比例函数y=$\frac{2}{x}$（x＞0）的图象上，有点P₁，P₂，P₃，…，P₂₀₁₀，它们的横坐标依次为1，2，3，…，2015．分别过这些点作
x轴与y轴的垂线，图中所构成的阴影部分的面积从左到右依次为S₁，
S₂，S₃，…，S₂₀₁₀，则S₁+S₂+S₃+…+S₂₀₁₅=$\frac{4030}{2016}$．

2．某工厂一种产品2013年的产量是100万件，计划2015年产量达到121万件．假设2013年到2015年这种产品产量的年增长率相同．
（1）求2013年到2015年这种产品产量的年增长率．
（2）若2016年产量还是按同样的增长率增长，预计2016年的产量是多少万件？

试题分类