题目内容
5.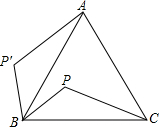 如图,P是等边三角形△ABC内的一点,连接PB、PC.若将△PBC绕点B旋转到△P′BA,则∠PBP′的度数是( )
如图,P是等边三角形△ABC内的一点,连接PB、PC.若将△PBC绕点B旋转到△P′BA,则∠PBP′的度数是( )| A. | 45° | B. | 60° | C. | 90° | D. | 120° |
分析 根据旋转的性质得到∠ABP′=∠CBP,根据等边三角形的性质得到∠ABC=60°,于是得到∠ABP′+∠ABP=60°,即可得到结论.
解答 解:∵将△PBC绕点B旋转到△P′BA,
∴∠ABP′=∠CBP,
∵△ABC是等边三角形,
∴∠ABC=60°,
∴∠ABP′+∠ABP=60°,
∴∠PBP′=60°,
故选B.
点评 本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了等边三角形的性质.

练习册系列答案
相关题目
16.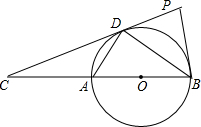 如图所示,直线CD与以线段AB为直径的圆相切于点D并交BA的延长线于点C,且AB=2,AD=1,P点在切线CD的延长线上移动时,则△PBD的外接圆的半径的最小值为( )
如图所示,直线CD与以线段AB为直径的圆相切于点D并交BA的延长线于点C,且AB=2,AD=1,P点在切线CD的延长线上移动时,则△PBD的外接圆的半径的最小值为( )
 如图所示,直线CD与以线段AB为直径的圆相切于点D并交BA的延长线于点C,且AB=2,AD=1,P点在切线CD的延长线上移动时,则△PBD的外接圆的半径的最小值为( )
如图所示,直线CD与以线段AB为直径的圆相切于点D并交BA的延长线于点C,且AB=2,AD=1,P点在切线CD的延长线上移动时,则△PBD的外接圆的半径的最小值为( )| A. | 1 | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{1}{2}$ | D. | $\sqrt{2}$ |
13.2015年6月国家主席习大大和比利时国王菲利普,在人民大会堂共同见证了两国公司在集成电路方面进行合作研发的签约仪式,两国将共同着力研发14纳米量产技术,这标志着我国芯片制造能力将进入国际顶尖水平.14纳米为0.000 000 014米,将0.000 000 014用科学记数法表示应为( )
| A. | 0.14×10-7 | B. | 1.4×10-8 | C. | 0.014×10-6 | D. | 14×10-9 |
20.与$-\sqrt{5}$是同类二次根式的是( )
| A. | $\sqrt{10}$ | B. | $\sqrt{15}$ | C. | $\sqrt{20}$ | D. | $\sqrt{25}$ |
17. 如图,△ABC内接于⊙O,连接OA,OB,∠C=40°,则∠OBA的度数是( )
如图,△ABC内接于⊙O,连接OA,OB,∠C=40°,则∠OBA的度数是( )
 如图,△ABC内接于⊙O,连接OA,OB,∠C=40°,则∠OBA的度数是( )
如图,△ABC内接于⊙O,连接OA,OB,∠C=40°,则∠OBA的度数是( )| A. | 60° | B. | 50° | C. | 45° | D. | 40° |
7.在下列以线段a,b,c的长为三边的三角形中,不能构成直角三角形的是( )
| A. | a=5,b=13,c=12 | B. | a=11,b=12,c=15 | C. | a:b:c=3:4:5 | D. | a=b=1,c=$\sqrt{2}$ |
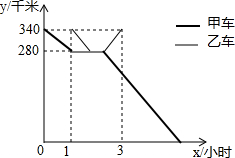 已知重庆和成都相距340千米,甲车早上八点从重庆出发往成都运送物资,行驶1小时后,汽车突然出现故障,立即通知技术人员乘乙车从重庆赶来维修(通知时间不计),乙车达到后经30分钟修好甲车,然后以原速返回重庆,同时甲车以原来速度的1.5倍继续前往成都.两车分别距离成都的路程y(千米)与甲车所用时间x(小时)之间的函数图象如图所示,下列四个结论:①甲车提速后的速度是90千米/时;②乙车的速度是70千米/时;③甲车修好的时间为10点15分;④甲车达到成都的时间为13点15分,其中,正确的结论是①③(填序号)
已知重庆和成都相距340千米,甲车早上八点从重庆出发往成都运送物资,行驶1小时后,汽车突然出现故障,立即通知技术人员乘乙车从重庆赶来维修(通知时间不计),乙车达到后经30分钟修好甲车,然后以原速返回重庆,同时甲车以原来速度的1.5倍继续前往成都.两车分别距离成都的路程y(千米)与甲车所用时间x(小时)之间的函数图象如图所示,下列四个结论:①甲车提速后的速度是90千米/时;②乙车的速度是70千米/时;③甲车修好的时间为10点15分;④甲车达到成都的时间为13点15分,其中,正确的结论是①③(填序号)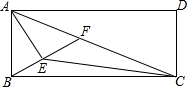 如图,在矩形ABCD中,AB=5,AD=12,AC是它的一条对角线,AE平分∠BAC,BE⊥AE于点E,交AC于点F,连接CE,则四边形AECD的面积是45.
如图,在矩形ABCD中,AB=5,AD=12,AC是它的一条对角线,AE平分∠BAC,BE⊥AE于点E,交AC于点F,连接CE,则四边形AECD的面积是45.