题目内容
14.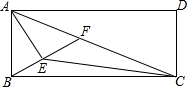 如图,在矩形ABCD中,AB=5,AD=12,AC是它的一条对角线,AE平分∠BAC,BE⊥AE于点E,交AC于点F,连接CE,则四边形AECD的面积是45.
如图,在矩形ABCD中,AB=5,AD=12,AC是它的一条对角线,AE平分∠BAC,BE⊥AE于点E,交AC于点F,连接CE,则四边形AECD的面积是45.
分析 先证明BE=EF,则S△ABE=S△AEF,S△BEC=S△EFC,所以S△ACE=$\frac{1}{2}$S△ABC,根据S四边形AECD=S△ACE+S△ADC即可解决问题.
解答 解:作FM⊥BC于M,
∵∠BAE=∠FAE,AE⊥BF,
∴∠BAE+∠ABF=90°,∠FAE+∠AFB=90°,
∴∠ABF=∠AFB,
∴AB=AF=5,
∵AE⊥EF,
∴BE=EF,
∵四边形ABCD是矩形,
∴AB=CD=5,BC=AD=12,∠D=90°,
∴S△ABC=S△ADC=$\frac{1}{2}$×5×12=30,
∴S△ABE=S△AEF,S△BEC=S△EFC,
∴S△ACE=$\frac{1}{2}$S△ABC=$\frac{1}{2}$•$\frac{1}{2}$•5•12=15,
∴S四边形AECD=S△ACE+S△ADC=15+30=45.
故答案为45.
点评 本题考查矩形的性质、三角形的面积、勾股定理等知识,解题的关键是学会利用分割法求四边形面积,属于中考常考题型.

练习册系列答案
相关题目
5.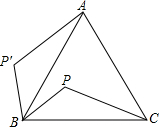 如图,P是等边三角形△ABC内的一点,连接PB、PC.若将△PBC绕点B旋转到△P′BA,则∠PBP′的度数是( )
如图,P是等边三角形△ABC内的一点,连接PB、PC.若将△PBC绕点B旋转到△P′BA,则∠PBP′的度数是( )
 如图,P是等边三角形△ABC内的一点,连接PB、PC.若将△PBC绕点B旋转到△P′BA,则∠PBP′的度数是( )
如图,P是等边三角形△ABC内的一点,连接PB、PC.若将△PBC绕点B旋转到△P′BA,则∠PBP′的度数是( )| A. | 45° | B. | 60° | C. | 90° | D. | 120° |
2.已知反比例函数y=$\frac{m}{x}$的图象位于二、四象限内,则关于x的方程(m+1)x2-2x+1=0根的情况是( )
| A. | 有一个或两个实数根 | B. | 仅有一个实数根 | ||
| C. | 有两个实数根 | D. | 没有实数根 |
9. 如图,数轴上有A,B,C,D四个点,其中表示绝对值相等的两个实数的点是( )
如图,数轴上有A,B,C,D四个点,其中表示绝对值相等的两个实数的点是( )
 如图,数轴上有A,B,C,D四个点,其中表示绝对值相等的两个实数的点是( )
如图,数轴上有A,B,C,D四个点,其中表示绝对值相等的两个实数的点是( )| A. | 点A与点D | B. | 点B 与点D | C. | 点B与点C | D. | 点C与点D |
19.据报道,截至2015年12月底,我区户籍人口突破90万.数据“90万”用科学记数法可表示为( )
| A. | 90×104 | B. | 9×104 | C. | 9×105 | D. | 0.9×105 |
16.下列各式,计算正确的是( )
| A. | $\sqrt{2}+\sqrt{3}=\sqrt{5}$ | B. | 3$\sqrt{3}-\sqrt{3}$=3 | C. | 2$\sqrt{5}×3\sqrt{5}=6\sqrt{5}$ | D. | ($\sqrt{8}-\sqrt{6}$)÷$\sqrt{2}$=2-$\sqrt{3}$ |
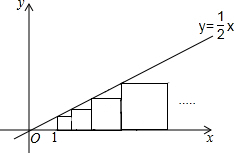 如图,在直线y=$\frac{1}{2}$x的下方依次作小正方形,每个小正方形的一个顶点都在直线y=$\frac{1}{2}$x上,若最小的正方形左边顶点的横坐标是1,则从左到右第10个小正方形的边长是$\frac{19683}{1024}$.
如图,在直线y=$\frac{1}{2}$x的下方依次作小正方形,每个小正方形的一个顶点都在直线y=$\frac{1}{2}$x上,若最小的正方形左边顶点的横坐标是1,则从左到右第10个小正方形的边长是$\frac{19683}{1024}$.