题目内容
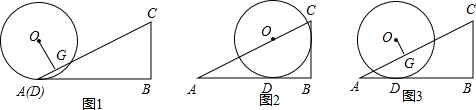
15.如图,△ABC中,∠B=90°,tan∠BAC=$\frac{1}{2}$,半径为2的⊙O从点A开始(图1),沿AB向右滚动,滚动时始终与AB相切(切点为D);当圆心O落在AC上时滚动停止,此时⊙O与BC相切于点E(图2).作OG⊥AC于点G.(1)利用图2,求cos∠BAC的值;
(2)当点D与点A重合时(如图1),求OG;
(3)如图3,在⊙O滚动过程中,设AD=x,请用含x的代数式表示OG,并写出x的取值范围.
分析 (1)连接OD,如图2所示,由圆O与AB相切,得到OD与AB垂直,根据tan∠BAC与OD的值,求出AD与OA的长,即可确定出cos∠BAC的值;
(2)如图1所示,连接OA,由圆O与AB相切,得到OA与AB垂直,再由OG垂直于AC,得到∠AOG与∠OAG互余,利用锐角三角函数定义求出OG的长即可;
(3)如图3所示,连接OD交AC于点F,由圆O与AB相切,得到OD与AB相切,利用切线的性质得到OD与AB垂直,根据OG与AC垂直,利用同角的余角相等得到∠FOG与∠BAC相等,利用锐角三角函数定义用x表示出OG,并求出x的范围即可.
解答  解:(1)如图2,连接OD,
解:(1)如图2,连接OD,
∵⊙O与AB相切,
∴OD⊥AB,
∵tan∠BAC=$\frac{1}{2}$,OD=2,
∴AD=4,OA=2$\sqrt{5}$,
∴cos∠BAC=$\frac{AD}{OA}$=$\frac{2\sqrt{5}}{5}$;
(2)如图1,连接OA,
∵⊙O与AB相切,
∴OA⊥AB,
又∵OG⊥AC,
∴∠AOG=∠BAC=90°-∠OAG,
∵cos∠AOG=$\frac{OG}{OA}$,
∴OG=OA•cos∠AOG=2×$\frac{2\sqrt{5}}{5}$=$\frac{4\sqrt{5}}{5}$;
(3)如图3,连接OD交AC于点F,
∵⊙O与AB相切,
∴OD⊥AB,
∴∠FOG=90°-∠OFG,
又∵OG⊥AC,
∴∠BAC=90°-∠AFD,
又∵∠FOG=∠AFD,
∴∠FOG=∠BAC,
∵tan∠BAC=$\frac{FD}{AD}$,
∴FD=AD•tan∠BAC=$\frac{1}{2}$x,
∴OF=2-$\frac{1}{2}$x,
∵cos∠BAC=cos∠FOG=$\frac{OG}{OF}$,
∴OG=OF•cos∠FOG=$\frac{2\sqrt{5}}{5}$(2-$\frac{1}{2}$x)=-$\frac{\sqrt{5}}{5}$x+$\frac{4\sqrt{5}}{5}$,x的取值范围是:0≤x≤4.
点评 此题属于圆综合题,涉及的知识有:切线的性质,锐角三角函数定义,熟练掌握切线的性质是解本题的关键.

 步步高达标卷系列答案
步步高达标卷系列答案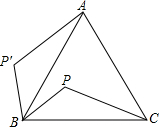 如图,P是等边三角形△ABC内的一点,连接PB、PC.若将△PBC绕点B旋转到△P′BA,则∠PBP′的度数是( )
如图,P是等边三角形△ABC内的一点,连接PB、PC.若将△PBC绕点B旋转到△P′BA,则∠PBP′的度数是( )| A. | 45° | B. | 60° | C. | 90° | D. | 120° |
 尺规作图:用直尺和圆规作图,不写作法,保留痕迹.
尺规作图:用直尺和圆规作图,不写作法,保留痕迹. 如图,在海中有一个小岛A,在它周围6n mile内有暗礁,渔船跟踪鱼群由西向东航行,在点B处测得小岛A在北偏东55方向,航行6n mlie到达C点,这时测得小岛A在北偏东29°方向上,如果渔船不改变航线继续向东航行,有没有触礁的危险.参考数据:tan29°≈0.55,tan35°≈0.70,tan55°≈1.43,tan61°≈1.80.
如图,在海中有一个小岛A,在它周围6n mile内有暗礁,渔船跟踪鱼群由西向东航行,在点B处测得小岛A在北偏东55方向,航行6n mlie到达C点,这时测得小岛A在北偏东29°方向上,如果渔船不改变航线继续向东航行,有没有触礁的危险.参考数据:tan29°≈0.55,tan35°≈0.70,tan55°≈1.43,tan61°≈1.80. 如图,在每个小正方形的边长为1的网格中,点A,B,C均在格点上.
如图,在每个小正方形的边长为1的网格中,点A,B,C均在格点上.