题目内容
20.与$-\sqrt{5}$是同类二次根式的是( )| A. | $\sqrt{10}$ | B. | $\sqrt{15}$ | C. | $\sqrt{20}$ | D. | $\sqrt{25}$ |
分析 根据化成最简二次根式后,被开方数相同的二次根式叫做同类二次根式.
解答 解:A、$\sqrt{10}$与-$\sqrt{5}$的被开方数不同,故A错误;
B、$\sqrt{15}$与-$\sqrt{5}$的被开方数不同,故B错误;
C、$\sqrt{20}=2\sqrt{5}$与-$\sqrt{5}$的被开方数相同,故C正确;
D、$\sqrt{25}=5$与-$\sqrt{5}$的被开方数不同,故D错误;
故选:C
点评 此题主要考查了同类二次根式的定义,即:化成最简二次根式后,被开方数相同的二次根式叫做同类二次根式.

练习册系列答案
相关题目
11.变量x,y有如下关系:①x+y=10;②y=$\frac{-5}{x}$;③y=|x-3|;④y2=8x,其中y是x的函数的是( )
| A. | ①②③④ | B. | ①②③ | C. | ①② | D. | ① |
8.化简$\frac{{x}^{2}}{x-1}$+$\frac{x}{1-x}$的结果是( )
| A. | x | B. | x-1 | C. | -x | D. | x+1 |
15.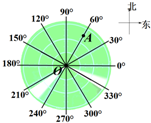 一艘海上搜救船借助雷达探测仪寻找到事故船的位置,雷达示意图如图所示,搜救船位于图中圆心O处,事故船位于距O点40海里的A处,雷达操作员要用方向角把事故船相对于搜救船的位置汇报给船长,以便调整航向,下列四种表述方式中正确的为( )
一艘海上搜救船借助雷达探测仪寻找到事故船的位置,雷达示意图如图所示,搜救船位于图中圆心O处,事故船位于距O点40海里的A处,雷达操作员要用方向角把事故船相对于搜救船的位置汇报给船长,以便调整航向,下列四种表述方式中正确的为( )
 一艘海上搜救船借助雷达探测仪寻找到事故船的位置,雷达示意图如图所示,搜救船位于图中圆心O处,事故船位于距O点40海里的A处,雷达操作员要用方向角把事故船相对于搜救船的位置汇报给船长,以便调整航向,下列四种表述方式中正确的为( )
一艘海上搜救船借助雷达探测仪寻找到事故船的位置,雷达示意图如图所示,搜救船位于图中圆心O处,事故船位于距O点40海里的A处,雷达操作员要用方向角把事故船相对于搜救船的位置汇报给船长,以便调整航向,下列四种表述方式中正确的为( )| A. | 事故船在搜救船的北偏东60°方向 | B. | 事故船在搜救船的北偏东30°方向 | ||
| C. | 事故船在搜救船的北偏西60°方向 | D. | 事故船在搜救船的南偏东30°方向 |
5.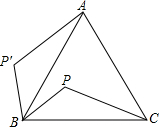 如图,P是等边三角形△ABC内的一点,连接PB、PC.若将△PBC绕点B旋转到△P′BA,则∠PBP′的度数是( )
如图,P是等边三角形△ABC内的一点,连接PB、PC.若将△PBC绕点B旋转到△P′BA,则∠PBP′的度数是( )
 如图,P是等边三角形△ABC内的一点,连接PB、PC.若将△PBC绕点B旋转到△P′BA,则∠PBP′的度数是( )
如图,P是等边三角形△ABC内的一点,连接PB、PC.若将△PBC绕点B旋转到△P′BA,则∠PBP′的度数是( )| A. | 45° | B. | 60° | C. | 90° | D. | 120° |
12.运用乘法公式计算(a+3)(a-3)的结果是( )
| A. | a2-6a+9 | B. | a2-3a+9 | C. | a2-9 | D. | a2-6a-9 |
9. 如图,数轴上有A,B,C,D四个点,其中表示绝对值相等的两个实数的点是( )
如图,数轴上有A,B,C,D四个点,其中表示绝对值相等的两个实数的点是( )
 如图,数轴上有A,B,C,D四个点,其中表示绝对值相等的两个实数的点是( )
如图,数轴上有A,B,C,D四个点,其中表示绝对值相等的两个实数的点是( )| A. | 点A与点D | B. | 点B 与点D | C. | 点B与点C | D. | 点C与点D |
 如图,在每个小正方形的边长为1的网格中,点A,B,C均在格点上.
如图,在每个小正方形的边长为1的网格中,点A,B,C均在格点上.