题目内容
16.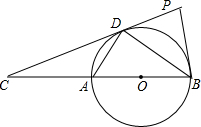 如图所示,直线CD与以线段AB为直径的圆相切于点D并交BA的延长线于点C,且AB=2,AD=1,P点在切线CD的延长线上移动时,则△PBD的外接圆的半径的最小值为( )
如图所示,直线CD与以线段AB为直径的圆相切于点D并交BA的延长线于点C,且AB=2,AD=1,P点在切线CD的延长线上移动时,则△PBD的外接圆的半径的最小值为( )| A. | 1 | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{1}{2}$ | D. | $\sqrt{2}$ |
分析 当BD为△PBD外接圆直径时,△PBD的外接圆半径最小,求出BD即可解决问题.
解答 解: 连接DO.
连接DO.
∵AB是直径,
∴∠ADB=90°,
∵AB=2,AD=1,
∴AB=2AD,
∴∠ABD=30°,
∵OD=OB,
∴∠ODB=∠OBD=30°,
∵CD是切线,
∴∠PDO=90°,
∴∠PDB=60°,
由题意当BD为△PBD外接圆直径时,△PBD的外接圆半径最小.
∵BD=$\sqrt{A{B}^{2}-A{D}^{2}}$=$\sqrt{3}$,
∴△PBD外接圆的半径为$\frac{\sqrt{3}}{2}$.
故选B.
点评 本题考查切线的性质、三角形外接圆的性质等知识,解题的关键是判断BD是△PBD外接圆的直径时,△PBD外接圆半径最小.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
11.变量x,y有如下关系:①x+y=10;②y=$\frac{-5}{x}$;③y=|x-3|;④y2=8x,其中y是x的函数的是( )
| A. | ①②③④ | B. | ①②③ | C. | ①② | D. | ① |
1.下列计算中,正确的是( )
| A. | (x4)4=x8 | B. | x3•x•x4=x7 | C. | (-2xy2)3=-6x3y6 | D. | (-x)5÷(-x)2=-x3 |
8.化简$\frac{{x}^{2}}{x-1}$+$\frac{x}{1-x}$的结果是( )
| A. | x | B. | x-1 | C. | -x | D. | x+1 |
5.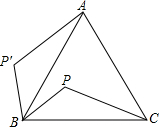 如图,P是等边三角形△ABC内的一点,连接PB、PC.若将△PBC绕点B旋转到△P′BA,则∠PBP′的度数是( )
如图,P是等边三角形△ABC内的一点,连接PB、PC.若将△PBC绕点B旋转到△P′BA,则∠PBP′的度数是( )
 如图,P是等边三角形△ABC内的一点,连接PB、PC.若将△PBC绕点B旋转到△P′BA,则∠PBP′的度数是( )
如图,P是等边三角形△ABC内的一点,连接PB、PC.若将△PBC绕点B旋转到△P′BA,则∠PBP′的度数是( )| A. | 45° | B. | 60° | C. | 90° | D. | 120° |
 尺规作图:用直尺和圆规作图,不写作法,保留痕迹.
尺规作图:用直尺和圆规作图,不写作法,保留痕迹.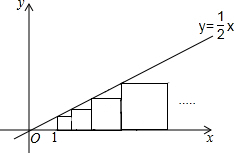 如图,在直线y=$\frac{1}{2}$x的下方依次作小正方形,每个小正方形的一个顶点都在直线y=$\frac{1}{2}$x上,若最小的正方形左边顶点的横坐标是1,则从左到右第10个小正方形的边长是$\frac{19683}{1024}$.
如图,在直线y=$\frac{1}{2}$x的下方依次作小正方形,每个小正方形的一个顶点都在直线y=$\frac{1}{2}$x上,若最小的正方形左边顶点的横坐标是1,则从左到右第10个小正方形的边长是$\frac{19683}{1024}$.