题目内容
17.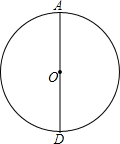 在学习圆与正多边形时,李晓露、马家骏两位同学设计了一个画圆内接正三角形的方法:
在学习圆与正多边形时,李晓露、马家骏两位同学设计了一个画圆内接正三角形的方法:①如图,作直径AD;
②作半径OD的垂直平分线,交⊙O于B,C两点;
③联结AB、AC、BC,那么△ABC为所求的三角形.
(1)请你按照两位同学设计的画法,画出△ABC.
(2)请你判断两位同学的作法是否正确?如果正确,给出△ABC是正三角形的证明过程;如果不正确,请说明理由.
分析 (1)作OD的垂直平分线得到弦BC,从而得到△ABC;
(2)连结CO,BC交AD于D,如图,由于BC垂直平分OD,易得OE=$\frac{1}{2}$OC,在Rt△OEC中,利用三角函数定义可求出∠OCE=30°,则∠COE=60°,再根据垂径定理得到$\widehat{AB}$=$\widehat{AC}$,$\widehat{BD}$=$\widehat{CD}$,则AB=AC,根据圆周角定理得到∠BAD=∠CAD=$\frac{1}{2}$∠COE=30°,即∠BAC=60°,于是可判断△ABC为等边三角形.
解答 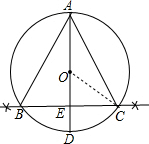 解:(1)如图;
解:(1)如图;
(2)两位同学的方法正确.
连结CO,BC交AD于D,如图,
∵BC垂直平分OD,
∴OE=$\frac{1}{2}$OD,即OE=$\frac{1}{2}$OC,
在Rt△OEC中,∵sin∠OCE=$\frac{OE}{OC}$=$\frac{1}{2}$,
∴∠OCE=30°,
∴∠COE=60°,
∵AD⊥BC,
∴$\widehat{AB}$=$\widehat{AC}$,$\widehat{BD}$=$\widehat{CD}$,
∴AB=AC,∠BAD=∠CAD=$\frac{1}{2}$∠COE=30°,
∴∠BAC=60°,
∴△ABC为等边三角形.
点评 本题考查了作图-复杂作图:复杂作图是在五种基本作图的基础上进行作图,一般是结合了几何图形的性质和基本作图方法.也考查了等边三角形的判定、垂径定理和圆周角定理.

练习册系列答案
相关题目
5.在平面直角坐标系内,点P(m-3,m-5)在第三象限,则m的取值范围是( )
| A. | -5<m<3 | B. | -3<m<5 | C. | m<3 | D. | m<5 |
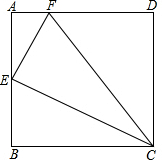 如图,已知四边形ABCD为正方形,E为AB中点,F为AD上的一点,且AF=$\frac{1}{4}$AD,试判断△EFC的形状,并说明理由.
如图,已知四边形ABCD为正方形,E为AB中点,F为AD上的一点,且AF=$\frac{1}{4}$AD,试判断△EFC的形状,并说明理由.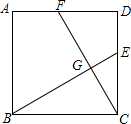 如图,点E、F是正方形ABCD中CD、AD边上的点,CE=DF,试判断BE与CF有怎样的关系?试说明为什么?
如图,点E、F是正方形ABCD中CD、AD边上的点,CE=DF,试判断BE与CF有怎样的关系?试说明为什么?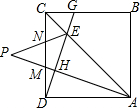 如图,在正方形ABCD中,点M、N是CD边上的两点,且DM=CN,过D作DG⊥AM于H,且分别交AC、BC于点E、G,AM、EN的延长线交于点P.
如图,在正方形ABCD中,点M、N是CD边上的两点,且DM=CN,过D作DG⊥AM于H,且分别交AC、BC于点E、G,AM、EN的延长线交于点P.
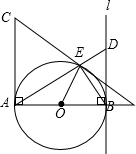 如图,AB=AC=8,∠BAC=90°,直线l与以AB为直径的⊙O相切于点B,点D是直线l上任意一动点,连接DA交⊙O于点E.
如图,AB=AC=8,∠BAC=90°,直线l与以AB为直径的⊙O相切于点B,点D是直线l上任意一动点,连接DA交⊙O于点E.