题目内容
6.如图1,某小区有一块空闲的梯形空地OABC,其中∠AOC=90°,OA=180m,OC=100m,BC=80m,为了改善居民的生活环境,同时满足居民停车的需要,物业公司决定对其进行改造,如图2建立直角坐标系.(1)求线段AB所在直线的函数解析式;
(2)物业公司的改造方案如下:在AB边上取一点P,过点P作PD⊥OA,PE⊥OC于E.划分出矩形ODPE部分修建花园,其余部分改造成停车场,居民要求花园的面积不得低于空地面积的60%,试通过计算说明,物业公司的改造方案是否可行;
(3)考虑到小区内行人的安全,有居民建立重新规划,将梯形空地划分的面积比为6:4的两部分,分别用于修建花园和停车场,物业公司决定采纳居民的建议,请你帮助物业公司设计一个改造方案,画出简图,并简要说明你的改造方案.

分析 (1)首先求出A、B两点的坐标,然后设线段AB所在直线的函数解析式是y=kx+b,把A、B两点的坐标代入,求出k、b的值是多少,即可确定出线段AB所在直线的函数解析式;
(2)首先作BN⊥OA与点N,BN与EP相交于点M,设EP=x,DP=y,则MP=x-80,NA=180-80=100,求出x+y=180,进而求出矩形ODPE的面积的最大值是多少;然后把它和梯形的面积的60%比较大小,判断出物业公司的改造方案是否可行即可.
(3)首先根据花园和停车场的面积比为6:4,求出花园的面积是多少;然后考虑到小区内行人的安全,可以设计一个长方形的花园和一个梯形的停车场,据此解答即可.
解答 解:(1)A点的坐标是(180,0),B点的坐标是(80,100),
设线段AB所在直线的函数解析式是y=kx+b,
则$\left\{\begin{array}{l}{0=180k+b}\\{100=80k+b}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=-1}\\{b=180}\end{array}\right.$,
∴线段AB所在直线的函数解析式是:
y=-x+180.
(2)如图1,作BN⊥OA与点N,BN与EP相交于点M,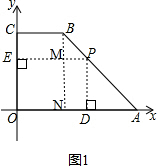 ,
,
设EP=x,DP=y,
则MP=x-80,NA=180-80=100,
∵$\frac{MP}{NA}=\frac{BM}{BN}$,
∴$\frac{x-80}{100}=\frac{100-y}{100}$,
∴x+y=180,
∴xy≤${(\frac{x+y}{2})}^{2}$=${(\frac{180}{2})}^{2}$=8100,
∵S梯形OABC=(80+180)×100÷2
=260×100÷2
=13000(平方米)
∴S梯形OABC×60%
=13000×0.6
=7800(平方米)
∵矩形ODPE的面积最大是8100平方米,8100>7800,
∴可以满足矩形ODPE的面积不低于空地面积的60%,
∴物业公司的改造方案可行.
(3)如图2,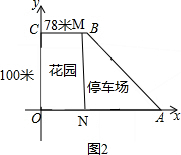 ,
,
∵13000×$\frac{6}{6+4}$
=13000×0.6
=7800(平方米)
∴花园的面积是7800平方米,
∵7800÷100=78(米),
∴可以设计一个长方形的花园CMNO,和一个梯形的停车场MBAN,
其中CM=ON=78米,MB=2米,NA=102米.
点评 (1)此题主要考查了一次函数综合题,考查了分析推理能力,考查了分类讨论思想的应用,考查了从已知函数图象中获取信息,并能利用获取的信息解答相应的问题的能力.
(2)此题还考查了直线的解析式的求法,以及梯形的面积的求法,还有两个数的最值的判断,要熟练掌握.


 在学习圆与正多边形时,李晓露、马家骏两位同学设计了一个画圆内接正三角形的方法:
在学习圆与正多边形时,李晓露、马家骏两位同学设计了一个画圆内接正三角形的方法: 老师出了如下的题:如图,要求在图中按下面的语言继续画图:(画图工具和方法不限)过A点画AD⊥BC于D,过D点画DE∥AB交AC于E,在线段AB上任取一点F,以F为顶点,FB为一边,画∠BFG=∠ADE,∠BFG的另一边FG与线段BC交于点G.请你按照上面画图时给出的条件说明FG⊥BC.
老师出了如下的题:如图,要求在图中按下面的语言继续画图:(画图工具和方法不限)过A点画AD⊥BC于D,过D点画DE∥AB交AC于E,在线段AB上任取一点F,以F为顶点,FB为一边,画∠BFG=∠ADE,∠BFG的另一边FG与线段BC交于点G.请你按照上面画图时给出的条件说明FG⊥BC.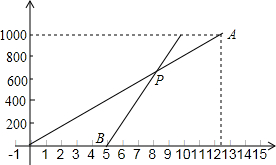 小明每天早上步行到学校上学,一天,小明从家里出发后5分钟,他爸爸发现他忘了带语文书,于是,爸爸立即以180米/分的速度沿相同路线去追小明,设小明离开家的时间为x(分),如图所示的线段OA表示小明从家到学校的过程中离开家的距离y1(米)与x(分)的关系;线段BP表示爸爸追赶小明时离开家的距离y2(米)与x(分)之间的关系.请分析图中的信息解答下列问题:
小明每天早上步行到学校上学,一天,小明从家里出发后5分钟,他爸爸发现他忘了带语文书,于是,爸爸立即以180米/分的速度沿相同路线去追小明,设小明离开家的时间为x(分),如图所示的线段OA表示小明从家到学校的过程中离开家的距离y1(米)与x(分)的关系;线段BP表示爸爸追赶小明时离开家的距离y2(米)与x(分)之间的关系.请分析图中的信息解答下列问题: