Question

7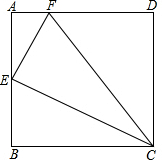．如图，已知四边形ABCD为正方形，E为AB中点，F为AD上的一点，且AF=$\frac{1}{4}$AD，试判断△EFC的形状，并说明理由．

Answer 1

分析 设AF=a，则FD=3a，DC=BC=4a，AE=EB=2a；在Rt△AEF、Rt△DFC，Rt△EBC中，利用勾股定理求出EF、EC、FC的长，再根据勾股定理的逆定理解答．

解答 解：如图：设AF=a，则FD=3a，DC=BC=4a，AE=EB=2a；
在Rt△AEF中，EF=$\sqrt{{a}^{2}+（2a）^{2}}$=$\sqrt{5}$a；
在Rt△DFC中，FC=$\sqrt{（3a）^{2}+（4a）^{2}}$=5a；
在Rt△EBC中，EC=$\sqrt{（2a）^{2}+（4a）^{2}}$=2$\sqrt{5}$a．
∴EC²+EF²=FC²，
∴△EFC是直角三角形．

点评 本题考查了勾股定理和勾股定理的逆定理及正方形的性质，利用勾股定理求出三角形三边长，再利用勾股定理逆定理解答，联合运用，是一道好题，值得关注．