题目内容
2.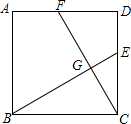 如图,点E、F是正方形ABCD中CD、AD边上的点,CE=DF,试判断BE与CF有怎样的关系?试说明为什么?
如图,点E、F是正方形ABCD中CD、AD边上的点,CE=DF,试判断BE与CF有怎样的关系?试说明为什么?
分析 如图,首先运用正方形的性质证明BC=CD,∠BCE=∠CDE;其次运用SAS公理证明△BCE≌△CDF,得到∠EBC=∠ECG,BE=CF;运用直角三角形的性质证明∠EGC=90°,即可解决问题.
解答  解:如图,BE⊥CF,BE=CF;
解:如图,BE⊥CF,BE=CF;
理由如下:
∵四边形ABCD为正方形,
∴BC=CD,∠BCE=∠CDE;
在△BCE与△CDF中,
$\left\{\begin{array}{l}{BC=CD}\\{∠BCE=∠CDF}\\{CE=DF}\end{array}\right.$,
∴△BCE≌△CDF(SAS),
∴∠EBC=∠ECG,BE=CF;
∵∠EBC+∠GEC=90°,
∴∠ECG+∠GEC=90,
∴∠EGC=90°,BE⊥CF,
∴BE=CF,且BE⊥CF.
点评 该题以正方形为载体,以考查正方形的性质、全等三角形的判定及其性质等几何知识点及其应用为核心构造而成;牢固掌握正方形的性质、全等三角形的判定及其性质等几何知识点是基础,灵活运用、解题是关键.

练习册系列答案
相关题目
10. 如图,正方形ABCD中,AE=AB,直线DE交BC于点F,则∠BEF=( )
如图,正方形ABCD中,AE=AB,直线DE交BC于点F,则∠BEF=( )
 如图,正方形ABCD中,AE=AB,直线DE交BC于点F,则∠BEF=( )
如图,正方形ABCD中,AE=AB,直线DE交BC于点F,则∠BEF=( )| A. | 35° | B. | 45° | C. | 55° | D. | 60° |
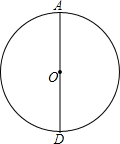 在学习圆与正多边形时,李晓露、马家骏两位同学设计了一个画圆内接正三角形的方法:
在学习圆与正多边形时,李晓露、马家骏两位同学设计了一个画圆内接正三角形的方法: 老师出了如下的题:如图,要求在图中按下面的语言继续画图:(画图工具和方法不限)过A点画AD⊥BC于D,过D点画DE∥AB交AC于E,在线段AB上任取一点F,以F为顶点,FB为一边,画∠BFG=∠ADE,∠BFG的另一边FG与线段BC交于点G.请你按照上面画图时给出的条件说明FG⊥BC.
老师出了如下的题:如图,要求在图中按下面的语言继续画图:(画图工具和方法不限)过A点画AD⊥BC于D,过D点画DE∥AB交AC于E,在线段AB上任取一点F,以F为顶点,FB为一边,画∠BFG=∠ADE,∠BFG的另一边FG与线段BC交于点G.请你按照上面画图时给出的条件说明FG⊥BC.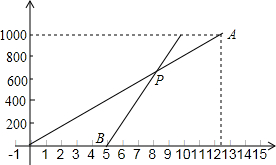 小明每天早上步行到学校上学,一天,小明从家里出发后5分钟,他爸爸发现他忘了带语文书,于是,爸爸立即以180米/分的速度沿相同路线去追小明,设小明离开家的时间为x(分),如图所示的线段OA表示小明从家到学校的过程中离开家的距离y1(米)与x(分)的关系;线段BP表示爸爸追赶小明时离开家的距离y2(米)与x(分)之间的关系.请分析图中的信息解答下列问题:
小明每天早上步行到学校上学,一天,小明从家里出发后5分钟,他爸爸发现他忘了带语文书,于是,爸爸立即以180米/分的速度沿相同路线去追小明,设小明离开家的时间为x(分),如图所示的线段OA表示小明从家到学校的过程中离开家的距离y1(米)与x(分)的关系;线段BP表示爸爸追赶小明时离开家的距离y2(米)与x(分)之间的关系.请分析图中的信息解答下列问题: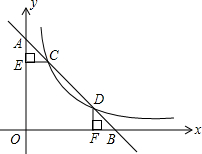 如图,一次函数的图象与x轴,y轴交于点B,A,与反比例函数y=$\frac{12}{x}$在第一象限内的图象交于点C(m,m+1),D(n,2),过点C作CE⊥y轴于点E,过点D作DF⊥x轴于点F.
如图,一次函数的图象与x轴,y轴交于点B,A,与反比例函数y=$\frac{12}{x}$在第一象限内的图象交于点C(m,m+1),D(n,2),过点C作CE⊥y轴于点E,过点D作DF⊥x轴于点F.