题目内容
17.如果(3+$\sqrt{3}$)2=a+b$\sqrt{3}$(a、b为实数),则a+b等于( )| A. | 9 | B. | 18 | C. | 12 | D. | 6 |
分析 根据(3+$\sqrt{3}$)2=a+b$\sqrt{3}$(a、b为实数),可以求得a、b的值,从而可以求得a+b的值.
解答 解:∵(3+$\sqrt{3}$)2=a+b$\sqrt{3}$
∴12+6$\sqrt{3}$=a+b$\sqrt{3}$
∴a=12,b=6,
∴a+b=12+6=18,
故选B.
点评 本题考查二次根式的化简求值,解题的关键是明确二次根式化简求值的方法.

练习册系列答案
相关题目
7.如果x2-x-1=(x-1)0,那么x的值为( )
| A. | 2或-1 | B. | 0或-1 | C. | 2 | D. | -1 |
2.矩形ABCD的面积是15,它的长与宽的比为3:1,则该矩形的宽为( )
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | $\sqrt{5}$ |
9.下列方程中,是关于x的一元二次方程的是( )
| A. | (x+1)2=2(x+1) | B. | $\frac{1}{{x}^{2}}$+$\frac{1}{x}$-2=0 | C. | ax2+bx+c=0 | D. | x2-2x=x2 |
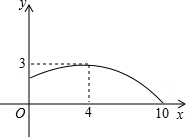 如图,一学生推铅球时,铅球行进高度y(m)与水平距离x(m)的函数图象为抛物线.
如图,一学生推铅球时,铅球行进高度y(m)与水平距离x(m)的函数图象为抛物线. 如图,在△ABC中,∠B=2∠C,BC═2AB,AD是中线,求证:△ABD是等边三角形.
如图,在△ABC中,∠B=2∠C,BC═2AB,AD是中线,求证:△ABD是等边三角形.