题目内容
8.在平面直角坐标系中,点P的坐标为(0,2),点M的坐标为(m-1,2m-4)(其中m为实数),当PM的长最小时,m的值为$\frac{13}{5}$.分析 由两点间的距离公式可得出PM2关于m的二次函数关系式,利用配方法结合二次函数的性质即可得出当PM取最小值时m的值.
解答 解:由两点间的距离公式可知:PM2=(m-1)2+(2m-4-2)2=5m2-26m+37=5$(m-\frac{13}{5})^{2}$+$\frac{16}{5}$,
∵5>0,
∴当m=$\frac{13}{5}$时,PM2最小.
故答案为:$\frac{13}{5}$.
点评 本题考查了两点间的距离公式以及二次函数的性质,解题的关键是找出PM2关于m的二次函数关系式.

练习册系列答案
 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
18.下列说法中正确的是( )
| A. | 有最小的自然数,也有最小的整数 | |
| B. | 没有最小的正数,但有最小的正整数 | |
| C. | 没有最小的负数,但有最小的正数 | |
| D. | 0是最小的整数 |
17.如果(3+$\sqrt{3}$)2=a+b$\sqrt{3}$(a、b为实数),则a+b等于( )
| A. | 9 | B. | 18 | C. | 12 | D. | 6 |
 如图,在正方形ABCD中,AB=2,E是AD边上一点(点E与点A,D不重合),BE的垂直平分线交AB于M,交DC于N,设AE=x.
如图,在正方形ABCD中,AB=2,E是AD边上一点(点E与点A,D不重合),BE的垂直平分线交AB于M,交DC于N,设AE=x.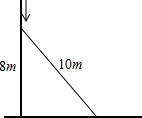 一个长为10m的梯子斜靠在墙上,梯子的顶端距地面的垂直距离为8m.
一个长为10m的梯子斜靠在墙上,梯子的顶端距地面的垂直距离为8m.