题目内容
11.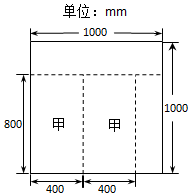 某装修公司为陶博会布置展厅,为了达到最佳装修效果,需用甲、乙两种型号的瓷砖.经计算,甲种型号瓷砖需用180块,乙种型号瓷砖需用120块,甲种型号瓷砖规格为800mm×400mm,乙种型号瓷砖规格为300mm×500mm,市场上只有同种花色的标准瓷砖,规格为1000mm×1000mm.一块标准瓷砖尽可能多的加工出甲、乙两种型号的瓷砖,公司共设计了三种加工方案(见下表).(图①是方案二的加工示意图)
某装修公司为陶博会布置展厅,为了达到最佳装修效果,需用甲、乙两种型号的瓷砖.经计算,甲种型号瓷砖需用180块,乙种型号瓷砖需用120块,甲种型号瓷砖规格为800mm×400mm,乙种型号瓷砖规格为300mm×500mm,市场上只有同种花色的标准瓷砖,规格为1000mm×1000mm.一块标准瓷砖尽可能多的加工出甲、乙两种型号的瓷砖,公司共设计了三种加工方案(见下表).(图①是方案二的加工示意图)| 方案一 | 方案二 | 方案三 | |
| 甲种型号瓷砖块数 | 1 | 2 | b |
| 乙种型号瓷砖块数 | a | 0 | 6 |
(1)表中a=4,b=0;
(2)分别求出y与x,z与x之间的函数关系式;
(3)若用W表示所购标准瓷砖的块数,求W与x的函数关系式,并指出当x取何值时W最小,此时按三种加工方案各加工多少块标准瓷砖?
分析 (1)根据题意可以得到a和b的值;
(2)根据表格中的数据可以解答本题;
(3)根据题意可以列出相应的函数,从而可以解答本题.
解答 解:(1)由题意可得,a=4,b=0,
故答案为:4,0;
(2)由题意可得,
x+2y=180,得y=90-0.5x,
4x+6z=120,得z=20-$\frac{2}{3}$x,
即y与x之间的函数关系式为y=90-0.5x,z与x之间的函数关系式为z=20-$\frac{2}{3}x$;
(3)由题意可得,
W=x+y+z=x+90-0.5x+20-$\frac{2}{3}x$=$-\frac{7}{6}x+110$,
∵$\left\{\begin{array}{l}{x≥0}\\{90-0.5x≥0}\\{20-\frac{2}{3}x≥0}\end{array}\right.$,
解得,0≤x≤30,
∴当x=30时,W取得最小值,此时W=75,y=75,z=0,
即W与x的函数关系式是W=$-\frac{7}{6}x+110$,当x取30时W最小,此时按三种加工方案各加工30块、75块、0块.
点评 本题考查一次函数的应用,解题的关键是明确题意,找出所求问题需要的条件.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,△ABC各顶点的坐标分别是A(-2,-4),B(0,-4),C(1,-1).
如图,△ABC各顶点的坐标分别是A(-2,-4),B(0,-4),C(1,-1). 如图:甲转盘被分成3个面积相等的扇形、乙转盘被分成2个面积相等的扇形.两圆心中心各有一个可以自由转动的指针,随机地转动指针(当指针指在边界线上时视为无效,重转).请回答下列问题.
如图:甲转盘被分成3个面积相等的扇形、乙转盘被分成2个面积相等的扇形.两圆心中心各有一个可以自由转动的指针,随机地转动指针(当指针指在边界线上时视为无效,重转).请回答下列问题.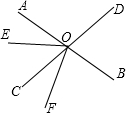 如图,直线AB、CD相交于点O.已知∠BOD=75°,OE把∠AOC分成两个角,且∠AOE:∠EOC=2:3.
如图,直线AB、CD相交于点O.已知∠BOD=75°,OE把∠AOC分成两个角,且∠AOE:∠EOC=2:3.