题目内容
1.已知一直线与直线y=-$\frac{1}{3}$x平行,且经过点(0,-5),则这条直线解析式为y=-$\frac{1}{3}$x-5.分析 由平行关系确定直线解析式的一次项系数,再将点(0,-5)代入求解析式的常数项.
解答 解:设所求直线解析式为y=kx+b,
∵所求直线平行于直线y=-$\frac{1}{3}$x,
∴k=-$\frac{1}{3}$,
将(0,-5)代入y=-$\frac{1}{3}$x+b中,得b=-5,
∴所求直线解析式为y=-$\frac{1}{3}$x-5,
故答案为:y=-$\frac{1}{3}$x-5.
点评 本题考查的是待定系数法求一次函数解析式.关键是根据直线与直线的平行关系确定一次项系数.

练习册系列答案
相关题目
9. 某校随机抽取了九年级的30名学生,测试了他们1分钟仰卧起坐的次数,并绘制如图所示的频数分布直方图,请根据图示计算,仰卧起坐次数在24.5~29.5之间的频率是( )
某校随机抽取了九年级的30名学生,测试了他们1分钟仰卧起坐的次数,并绘制如图所示的频数分布直方图,请根据图示计算,仰卧起坐次数在24.5~29.5之间的频率是( )
 某校随机抽取了九年级的30名学生,测试了他们1分钟仰卧起坐的次数,并绘制如图所示的频数分布直方图,请根据图示计算,仰卧起坐次数在24.5~29.5之间的频率是( )
某校随机抽取了九年级的30名学生,测试了他们1分钟仰卧起坐的次数,并绘制如图所示的频数分布直方图,请根据图示计算,仰卧起坐次数在24.5~29.5之间的频率是( )| A. | 0.1 | B. | 0.17 | C. | 0.33 | D. | 0.4 |
9.关于三角形的角平分线和中线,下列说法正确的是( )
| A. | 都是直线 | B. | 都是射线 | ||
| C. | 都是线段 | D. | 可以是射线也可以是线段 |
16.火车票上的车次号有两个意义,一是数字越小表示车速快,1~98次为特快列车,101~198次为直快列车,301~398次为普快列车,401~498次为普客列车;二是单数与双数表示不同的行驶方向,其中单数表示从北京开出,双数表示开往北京.根据以上规定,北京开往杭州的某一直快列车的车次号可能是( )
| A. | 20 | B. | 119 | C. | 120 | D. | 319 |
11.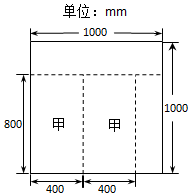 某装修公司为陶博会布置展厅,为了达到最佳装修效果,需用甲、乙两种型号的瓷砖.经计算,甲种型号瓷砖需用180块,乙种型号瓷砖需用120块,甲种型号瓷砖规格为800mm×400mm,乙种型号瓷砖规格为300mm×500mm,市场上只有同种花色的标准瓷砖,规格为1000mm×1000mm.一块标准瓷砖尽可能多的加工出甲、乙两种型号的瓷砖,公司共设计了三种加工方案(见下表).(图①是方案二的加工示意图)
某装修公司为陶博会布置展厅,为了达到最佳装修效果,需用甲、乙两种型号的瓷砖.经计算,甲种型号瓷砖需用180块,乙种型号瓷砖需用120块,甲种型号瓷砖规格为800mm×400mm,乙种型号瓷砖规格为300mm×500mm,市场上只有同种花色的标准瓷砖,规格为1000mm×1000mm.一块标准瓷砖尽可能多的加工出甲、乙两种型号的瓷砖,公司共设计了三种加工方案(见下表).(图①是方案二的加工示意图)
设购买的标准瓷砖全部加工完,其中按方案一加工x块,按方案二加工y块,按方案三加工z块,且加工好的甲、乙两种型号瓷砖刚好够用.
(1)表中a=4,b=0;
(2)分别求出y与x,z与x之间的函数关系式;
(3)若用W表示所购标准瓷砖的块数,求W与x的函数关系式,并指出当x取何值时W最小,此时按三种加工方案各加工多少块标准瓷砖?
 某装修公司为陶博会布置展厅,为了达到最佳装修效果,需用甲、乙两种型号的瓷砖.经计算,甲种型号瓷砖需用180块,乙种型号瓷砖需用120块,甲种型号瓷砖规格为800mm×400mm,乙种型号瓷砖规格为300mm×500mm,市场上只有同种花色的标准瓷砖,规格为1000mm×1000mm.一块标准瓷砖尽可能多的加工出甲、乙两种型号的瓷砖,公司共设计了三种加工方案(见下表).(图①是方案二的加工示意图)
某装修公司为陶博会布置展厅,为了达到最佳装修效果,需用甲、乙两种型号的瓷砖.经计算,甲种型号瓷砖需用180块,乙种型号瓷砖需用120块,甲种型号瓷砖规格为800mm×400mm,乙种型号瓷砖规格为300mm×500mm,市场上只有同种花色的标准瓷砖,规格为1000mm×1000mm.一块标准瓷砖尽可能多的加工出甲、乙两种型号的瓷砖,公司共设计了三种加工方案(见下表).(图①是方案二的加工示意图)| 方案一 | 方案二 | 方案三 | |
| 甲种型号瓷砖块数 | 1 | 2 | b |
| 乙种型号瓷砖块数 | a | 0 | 6 |
(1)表中a=4,b=0;
(2)分别求出y与x,z与x之间的函数关系式;
(3)若用W表示所购标准瓷砖的块数,求W与x的函数关系式,并指出当x取何值时W最小,此时按三种加工方案各加工多少块标准瓷砖?
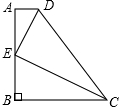 如图,已知CB⊥AB,点E在AB上,且CE平分∠BCD,DE平分∠ADC,∠EDC+∠DCE=90°,求证:DA⊥AB.
如图,已知CB⊥AB,点E在AB上,且CE平分∠BCD,DE平分∠ADC,∠EDC+∠DCE=90°,求证:DA⊥AB.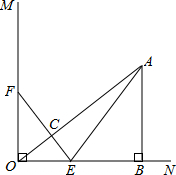 如图,已知∠MON=90°,A是∠MON内部的一点,过点A作AB⊥ON,垂足为点B,AB=3厘米,OB=4厘米,动点E,F同时从O点出发,点E以1.5厘米/秒的速度沿ON方向运动,点F以2厘米/秒的速度OM方向运动,EF与OA交于点C,连接AE,当点E到达点B时,点F随之停止运动.设运动时间为t秒(t>0)
如图,已知∠MON=90°,A是∠MON内部的一点,过点A作AB⊥ON,垂足为点B,AB=3厘米,OB=4厘米,动点E,F同时从O点出发,点E以1.5厘米/秒的速度沿ON方向运动,点F以2厘米/秒的速度OM方向运动,EF与OA交于点C,连接AE,当点E到达点B时,点F随之停止运动.设运动时间为t秒(t>0)