题目内容
12.如果有理数a、b、c满足,a+b+c=0,abc>0,那么a、b、c中负数的个数是2.分析 先根据abc>0,结合有理数乘法法则,易知a、b、c中有2个负数或没有一个负数(都是正数),而都是正数,则a+b+c>0,不符合a+b+c=0的要求,于是可得a、b、c中必有2个负数.
解答 解:∵abc>0,
∴a、b、c中有2个负数或没有一个负数,
若没有一个负数,则a+b+c>0,不符合a+b+c=0的要求,
故a、b、c中必有2个负数.
故答案为:2.
点评 本题考查了有理数的乘法、有理数的加法法则.解题的关键是分情况讨论问题.

练习册系列答案
相关题目
20. 如图OP平分∠AOB,PC⊥OA于C,D在OB上,PC=3,则PD的大小关系是( )
如图OP平分∠AOB,PC⊥OA于C,D在OB上,PC=3,则PD的大小关系是( )
 如图OP平分∠AOB,PC⊥OA于C,D在OB上,PC=3,则PD的大小关系是( )
如图OP平分∠AOB,PC⊥OA于C,D在OB上,PC=3,则PD的大小关系是( )| A. | PD≥3 | B. | PD=3 | C. | PD≤3 | D. | 不能确定 |
7. 如图,有A、B、C、D四个小岛,A、B、C在同一条直线上,而且B、C在A的正东方,D岛在C岛的正北方,A岛在D岛的南偏西52°方向,B岛在D岛的南偏东40°方向.那么∠DAC和∠DBC分别是多少?
如图,有A、B、C、D四个小岛,A、B、C在同一条直线上,而且B、C在A的正东方,D岛在C岛的正北方,A岛在D岛的南偏西52°方向,B岛在D岛的南偏东40°方向.那么∠DAC和∠DBC分别是多少?
 如图,有A、B、C、D四个小岛,A、B、C在同一条直线上,而且B、C在A的正东方,D岛在C岛的正北方,A岛在D岛的南偏西52°方向,B岛在D岛的南偏东40°方向.那么∠DAC和∠DBC分别是多少?
如图,有A、B、C、D四个小岛,A、B、C在同一条直线上,而且B、C在A的正东方,D岛在C岛的正北方,A岛在D岛的南偏西52°方向,B岛在D岛的南偏东40°方向.那么∠DAC和∠DBC分别是多少?
4.满足方程$\frac{1}{x-2}+3=\frac{x-1}{x-2}$的x的值是( )
| A. | x=2 | B. | x=-2 | C. | x=0 | D. | 无解 |
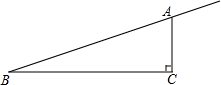 如图,在Rt△ABC中,∠ACB=90°,AC=1cm,BC=4cm,动点P从点B出发,以每秒1cm的速度沿射线BA运动,求出点P运动所有的时间,使得△PBC为等腰三角形.
如图,在Rt△ABC中,∠ACB=90°,AC=1cm,BC=4cm,动点P从点B出发,以每秒1cm的速度沿射线BA运动,求出点P运动所有的时间,使得△PBC为等腰三角形. 一个零件的形状如图所示,按规定∠A应等于90°,∠B、∠D应分别是25°和35°,李叔叔量得∠BCD是多少时,才能断定这个零件是合格的,你能说出道理吗?
一个零件的形状如图所示,按规定∠A应等于90°,∠B、∠D应分别是25°和35°,李叔叔量得∠BCD是多少时,才能断定这个零件是合格的,你能说出道理吗?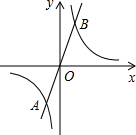 如图,反比例函数y1=$\frac{{k}_{1}}{x}$与正比例函数y2=k2c相交于点A(-1,-3)和点B.
如图,反比例函数y1=$\frac{{k}_{1}}{x}$与正比例函数y2=k2c相交于点A(-1,-3)和点B.