题目内容
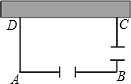
20．
如图OP平分∠AOB，PC⊥OA于C，D在OB上，PC=3，则PD的大小关系是（ ）| A． | PD≥3 | B． | PD=3 | C． | PD≤3 | D． | 不能确定 |
分析 过点P作PE⊥OB于E，根据角平分线上的点到角的两边距离相等可得PE=PC，再根据垂线段最短解答．
解答 
解：如图，过点P作PE⊥OB于E，
∵OP平分∠AOB，PC⊥OA，
∴PE=PC=3，
∵D在OB上，
∴PD≥PE，
∴PD≥3．
故选A．
点评 本题考查了角平分线上的点到角的两边距离相等的性质，垂线段最短的性质，熟记性质是解题的关键，作出辅助线更形象直观．
练习册系列答案
相关题目
10．已知2x-5y=0，则$\frac{x}{x+y}$=（ ）
| A． | $\frac{5}{7}$ | B． | $\frac{2}{7}$ | C． | $\frac{2}{5}$ | D． | $\frac{3}{5}$ |
11．下列说法错误的是（ ）
| A． | 平面上到角的两边的距离相等的点一定在角的平分线上 | |
| B． | 角平分线上任一点到角的两边的距离一定相等 | |
| C． | 一个角只有一条角平分线 | |
| D． | 一个角有无数条角平分线 |
配方法不仅可以用来解一元二次方程，还可以用来解决很多问题．
如图，点O是等边△ABC内一点，∠AOB=100°，∠BOC=α．以OC为一边作等边三角形OCD，连接AC、AD．