题目内容
1.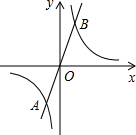 如图,反比例函数y1=$\frac{{k}_{1}}{x}$与正比例函数y2=k2c相交于点A(-1,-3)和点B.
如图,反比例函数y1=$\frac{{k}_{1}}{x}$与正比例函数y2=k2c相交于点A(-1,-3)和点B.(1)求k1,k2的值;
(2)写出点B的坐标;
(3)写出$\frac{{k}_{1}}{x}$>k2x的解集.
分析 (1)由正比例函数与反比例函数图象的交点为点A(-1,-3),将点A(-1,-3)代入正比例函数解析式中求出k1的值,代入反比例函数解析式中求出k2的值;
(2)由于正比例函数与反比例函数的图象均关于原点对称,所以A、B两点关于原点对称,由关于原点对称的点的坐标特点求出B点坐标即可.
(3)根据函数的图象和交点坐标即可求得$\frac{{k}_{1}}{x}$>k2x的解集.
解答 解:(1)由(-1,-3)为正比例与反比例函数图象的交点,
将x=-1,y=-3代入y1=$\frac{{k}_{1}}{x}$得:k1=3,
将x=-1,y=-3代入y2=k2x得:k2=3;
(2)∵正比例函数与反比例函数的图象均关于原点对称,
∴A、B两点关于原点对称,
∵A的坐标为(-1,-3),
∴B的坐标为(1,3).
(3)$\frac{{k}_{1}}{x}$>k2x的解集为:x<-1或0<x<1.
点评 此题考查了反比例函数与一次函数的交点问题,待定系数法求函数解析式和图象上点的坐标,并结合图象看不等式的解,关键掌握凡是图象经过的点都能满足解析式,利用代入法即可求出解析式或点的坐标.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.下列说法错误的是( )
| A. | 平面上到角的两边的距离相等的点一定在角的平分线上 | |
| B. | 角平分线上任一点到角的两边的距离一定相等 | |
| C. | 一个角只有一条角平分线 | |
| D. | 一个角有无数条角平分线 |
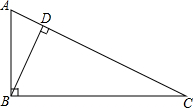 如图,在△ABC中,∠ABC=90°,△ABC∽△BDC,AB=3,AC=5,求DC的长.
如图,在△ABC中,∠ABC=90°,△ABC∽△BDC,AB=3,AC=5,求DC的长.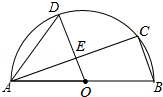 如图,AB是半圆O的直径,C、D是半圆O上的两点,且OD∥BC,OD与AC交于点E.
如图,AB是半圆O的直径,C、D是半圆O上的两点,且OD∥BC,OD与AC交于点E.