题目内容
2.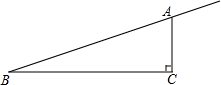 如图,在Rt△ABC中,∠ACB=90°,AC=1cm,BC=4cm,动点P从点B出发,以每秒1cm的速度沿射线BA运动,求出点P运动所有的时间,使得△PBC为等腰三角形.
如图,在Rt△ABC中,∠ACB=90°,AC=1cm,BC=4cm,动点P从点B出发,以每秒1cm的速度沿射线BA运动,求出点P运动所有的时间,使得△PBC为等腰三角形.
分析 根据勾股定理求出斜边AB,根据等腰三角形的判定得出符合情况的三种情况:①BP=PC,②BP=BC,③BC=CP,根据等腰三角形的性质得出即可.
解答 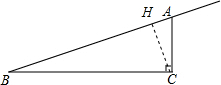 解:在Rt△ABC中,∠ACB=90°,AC=1cm,BC=4cm,
解:在Rt△ABC中,∠ACB=90°,AC=1cm,BC=4cm,
∴AB=$\sqrt{17}$cm,
设BP=t,且△PBC为等腰三角形有三种可能:
①若BP=PC,则∠B=∠PCB,
∵∠ACB=90°,
∴∠PAC=∠PCA,
∴PC=PA,
∴t=BP=$\frac{1}{2}$AB=$\frac{\sqrt{17}}{2}$;
②若BP=BC,则t=4;
③若BC=PC,过点C作CH⊥AB,如图,
则BP=2BH.由CH•AB=BC•AC,得CH=$\frac{BC•AC}{AB}$=$\frac{4×1}{\sqrt{17}}$=$\frac{4\sqrt{17}}{17}$;
在Rt△BHC中,由勾股定理得BH=$\sqrt{B{C}^{2}-C{H}^{2}}$=$\frac{16\sqrt{17}}{17}$,
∴t=BP=$\frac{32\sqrt{17}}{17}$;
综上所述,符合要求的t的值有3个,分别是$\frac{\sqrt{17}}{2}$秒或4秒$\frac{32\sqrt{17}}{17}$秒.
点评 本题考查了等腰三角形的性质和判定,勾股定理,三角形的面积的应用,能求出符合情况的所有情况是解此题的关键,用了分类讨论思想.

练习册系列答案
相关题目
10.已知2x-5y=0,则$\frac{x}{x+y}$=( )
| A. | $\frac{5}{7}$ | B. | $\frac{2}{7}$ | C. | $\frac{2}{5}$ | D. | $\frac{3}{5}$ |
17.以下列各组线段为边,能组成三角形的是( )
| A. | 4cm,6cm,8cm | B. | 2cm,3cm,5cm | C. | 5cm,6cm,12cm | D. | 1cm,2cm,4cm |
7.如图所示,在餐桌上摆碗,一张餐桌上放6个碗,2张餐桌上放12个碗,按图继续排列餐桌并摆碗.

填写表格:

填写表格:
| 桌子的张数 | 1 | 2 | 3 | 4 | … | n |
| 摆碗数 | 6 | 12 | 18 | 24 | 6n |
14.下列各式,计算正确的是( )
| A. | (-2)3=-23 | B. | -14=(-1)4 | C. | 32=23 | D. | (-1)3=-3 |
11.下列说法错误的是( )
| A. | 平面上到角的两边的距离相等的点一定在角的平分线上 | |
| B. | 角平分线上任一点到角的两边的距离一定相等 | |
| C. | 一个角只有一条角平分线 | |
| D. | 一个角有无数条角平分线 |
 如图,已知AB=AC,BD=DC,AD的延长线交BC于点E.
如图,已知AB=AC,BD=DC,AD的延长线交BC于点E.