题目内容
2.在7:00到8:00之间,何时分针与时针:(1)成平角;(2)重合;(3)成直角.分析 首先求出时针与分针的运动速度,然后根据题意;(1)成平角;(2)重合;(3)成直角;列出方程,问题即可解决.
解答 解:由题意得:时针的转动速度为0.5°/分钟,
分针的转动速度为6°/分钟,
设时针与分针的转动时间为t分钟;
(1)时针与分针成平角,
30×7+0.5×t-6t=180,
解得t=$\frac{60}{11}$,
即7时$\frac{60}{11}$分时针与分针成平角;
(2)当时针与分针重合时,
30×7+0.5t-6t=0
解得:t=$\frac{420}{11}$,
故在7时$\frac{420}{11}$分,钟的时针与分针重合.
(3)30×7+0.5t-6t=90
解得:t=$\frac{240}{11}$,
故在7时$\frac{240}{11}$分,钟的时针与分针成直角;
6t-(30×7+0.5t)=90,
解得:t=$\frac{600}{11}$.
故在7时$\frac{600}{11}$分,钟的时针与分针成直角;
综上所述:.在7时$\frac{240}{11}$分或在7时$\frac{600}{11}$分,钟的时针与分针成直角.
点评 该题主要考查了钟面角,利用一元一次方程及其应用问题,解题的关键是根据时针与分针的运动速度,正确列出方程,准确求解运算

练习册系列答案
相关题目
12.若a<0,ab<0,则|b-a+1|-|a-b-4|的值( )
| A. | 3 | B. | -3 | C. | 2b-2a+5 | D. | 不能确定 |
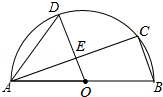 如图,AB是半圆O的直径,C、D是半圆O上的两点,且OD∥BC,OD与AC交于点E.
如图,AB是半圆O的直径,C、D是半圆O上的两点,且OD∥BC,OD与AC交于点E.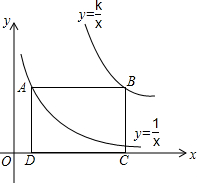 如图,点A在双曲线y=$\frac{1}{x}$上,点B在双曲线y=$\frac{k}{x}$上,且AB∥x轴,C,D两点在x轴上.若矩形ABCD的面积为6,求B点所在双曲线的函数表达式.
如图,点A在双曲线y=$\frac{1}{x}$上,点B在双曲线y=$\frac{k}{x}$上,且AB∥x轴,C,D两点在x轴上.若矩形ABCD的面积为6,求B点所在双曲线的函数表达式. 如图,△ABC中,点D在BC上,EF∥BC,分别交AB,AC,AD于点E,F,G,图中共有几对相似三角形?分别是哪几对?
如图,△ABC中,点D在BC上,EF∥BC,分别交AB,AC,AD于点E,F,G,图中共有几对相似三角形?分别是哪几对?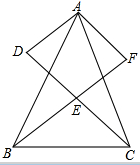 如图,△ADC≌△AFB,∠DAB=20°,DA∥BF,DC,BF交于点E.
如图,△ADC≌△AFB,∠DAB=20°,DA∥BF,DC,BF交于点E.