题目内容
6.最简根式$\root{5a+b}{3a-b}$与-$\root{4-a}{7a+b}$是同类根式,求$\root{5a+b}{3a-b}$-2$\root{4-a}{7a+b}$的值.分析 根据同类二次根式是化为最简二次根式后,被开方数相同的二次根式称为同类二次根式,可得关于a、b的二元一次方程组,根据解方程组,可得具体的同类二次根式,根据二次根式的加减,可得答案.
解答 解:由最简根式$\root{5a+b}{3a-b}$与-$\root{4-a}{7a+b}$是同类根式,得
$\left\{\begin{array}{l}{5a+b=4-a}\\{3a-b=7a+b}\end{array}\right.$.
解得$\left\{\begin{array}{l}{a=1}\\{b=-2}\end{array}\right.$,
$\root{5a+b}{3a-b}$-2$\root{4-a}{7a+b}$=$\sqrt{5}$-2$\sqrt{5}$=-$\sqrt{5}$.
点评 本题考查了同类二次根式,利用同类二次根式得出关于a、b的方程组是解题关键.

练习册系列答案
相关题目
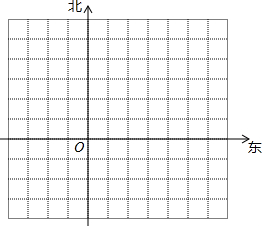 小强放学后,先向东走了300米,再向北走路200米,到书店A买了一本书,然后向西走了500米,再向南走了100米,到快餐店B买了零食,又向南走了400米,再向东走了800米,回到他家C,如图,以学校为原点建立坐标系,图中的每个单位长度表示100米.
小强放学后,先向东走了300米,再向北走路200米,到书店A买了一本书,然后向西走了500米,再向南走了100米,到快餐店B买了零食,又向南走了400米,再向东走了800米,回到他家C,如图,以学校为原点建立坐标系,图中的每个单位长度表示100米.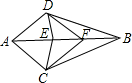 如图,已知AC=AD,BC=BD,CE=DE,则全等三角形共有6对.
如图,已知AC=AD,BC=BD,CE=DE,则全等三角形共有6对. 如图,P是△ABC内一点,延长BP交AC于点D,若∠3=25°,∠A=67°,∠4=40°,则∠1的度数是多少?
如图,P是△ABC内一点,延长BP交AC于点D,若∠3=25°,∠A=67°,∠4=40°,则∠1的度数是多少? 如图,已知AC与BD相交于点O,AD∥BC,且AO=OD.求证:OB=OC.
如图,已知AC与BD相交于点O,AD∥BC,且AO=OD.求证:OB=OC.