题目内容
1.(1)证明:$\sqrt{{a}^{2}+\frac{1}{{b}^{2}}+\frac{{a}^{2}}{(ab+1)^{2}}}$=|a+$\frac{1}{b}$-$\frac{a}{ab+1}$|;(2)利用(1)式,计算$\sqrt{1+199{0}^{2}+\frac{199{0}^{2}}{199{1}^{2}}}$-$\frac{1}{1991}$.
分析 (1)根据完全平方公式,可得答案.
(2)根据$\sqrt{{a}^{2}+\frac{1}{{b}^{2}}+\frac{{a}^{2}}{(ab+1)^{2}}}$=|a+$\frac{1}{b}$-$\frac{a}{ab+1}$|,可得答案.
解答 (1)证明:∵(a+$\frac{1}{b}$-$\frac{a}{ab+1}$)2
=a2+$\frac{1}{{b}^{2}}$+$\frac{{a}^{2}}{(ab+1)^{2}}$+$\frac{2a}{b}$-$\frac{2{a}^{2}}{ab+1}$-$\frac{2a}{b(ab+1)}$
=a2+$\frac{1}{{b}^{2}}$+$\frac{2a(ab+1)-2a{b}^{2}-2a}{b(ab+1)}$
=a2+$\frac{1}{{b}^{2}}$+$\frac{{a}^{2}}{(ab+1)^{2}}$,
∴原式成立;
(2)原式=$\sqrt{199{0}^{2}+\frac{1}{{1}^{2}}+\frac{199{0}^{2}}{1990×1+1}}$-$\frac{1}{1991}$=1990+$\frac{1}{1}$-$\frac{1990}{1990×1+1}$-$\frac{1}{1991}$
=1990+1-1
=1990.
点评 本题考查了二次根式的性质与化简,利用完全平方公式是解题关键.

练习册系列答案
相关题目
12.下列说法:①用同一张底片冲洗出来的8张1寸相片是全等形;②我国国旗上的四颗小五角星是全等形;③所有的等边三角形是全等形;④全等形的面积一定相等,其中正确的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
16. 王师傅用4根木条钉成一个四边形木架,如图,要使这个木架不变形,他至少还要再钉上木条的条数为( )
王师傅用4根木条钉成一个四边形木架,如图,要使这个木架不变形,他至少还要再钉上木条的条数为( )
 王师傅用4根木条钉成一个四边形木架,如图,要使这个木架不变形,他至少还要再钉上木条的条数为( )
王师傅用4根木条钉成一个四边形木架,如图,要使这个木架不变形,他至少还要再钉上木条的条数为( )| A. | 0根 | B. | 1根 | C. | 2根 | D. | 3根 |
 有一个数值转换器,原理如图所示,当输入的数为16时,输出的数为$\sqrt{2}$.
有一个数值转换器,原理如图所示,当输入的数为16时,输出的数为$\sqrt{2}$.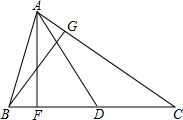 如图,△ABC的边BC上的高为AF,中线为AD,AC边上的高为BG,已知AF=6,BC=10,BG=5.
如图,△ABC的边BC上的高为AF,中线为AD,AC边上的高为BG,已知AF=6,BC=10,BG=5. 如图.在2×3的正方形网格中,小正方形的边长为1,以图中A、B、C、D、E中的三点为顶点的三角形中,面积为1的三角形有哪些?
如图.在2×3的正方形网格中,小正方形的边长为1,以图中A、B、C、D、E中的三点为顶点的三角形中,面积为1的三角形有哪些?