题目内容
3.已知$\frac{x}{2}$=$\frac{y}{5}$,则$\frac{x+y}{x}$的值为$\frac{7}{2}$.分析 求出x=$\frac{2}{5}$y,代入即可求出答案.
解答 解:∵$\frac{x}{2}$=$\frac{y}{5}$,
∴x=$\frac{2}{5}$y,
∴$\frac{x+y}{x}$=$\frac{\frac{2}{5}y+y}{\frac{2}{5}y}$=$\frac{7}{2}$,
故答案为:$\frac{7}{2}$.
点评 本题考查了比例的性质的应用,能根据比例的性质求出x=$\frac{2}{5}$y是解此题的关键.

练习册系列答案
相关题目
13.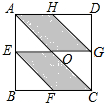 如图,正方形ABCD是一块绿化带,E,F,G,H分别是AB,BC,CD,AD的中点,阴影部分EOCF,AOGH都是花圃,一只自由飞翔的小鸟,将随机落在这块绿化带上,则小鸟在花圃上的概率为( )
如图,正方形ABCD是一块绿化带,E,F,G,H分别是AB,BC,CD,AD的中点,阴影部分EOCF,AOGH都是花圃,一只自由飞翔的小鸟,将随机落在这块绿化带上,则小鸟在花圃上的概率为( )
 如图,正方形ABCD是一块绿化带,E,F,G,H分别是AB,BC,CD,AD的中点,阴影部分EOCF,AOGH都是花圃,一只自由飞翔的小鸟,将随机落在这块绿化带上,则小鸟在花圃上的概率为( )
如图,正方形ABCD是一块绿化带,E,F,G,H分别是AB,BC,CD,AD的中点,阴影部分EOCF,AOGH都是花圃,一只自由飞翔的小鸟,将随机落在这块绿化带上,则小鸟在花圃上的概率为( )| A. | $\frac{1}{2}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{3}$ | D. | $\frac{2}{5}$ |
14. 如图:AB=DC,要使△ABC≌△DCB,不能添加的条件是( )
如图:AB=DC,要使△ABC≌△DCB,不能添加的条件是( )
 如图:AB=DC,要使△ABC≌△DCB,不能添加的条件是( )
如图:AB=DC,要使△ABC≌△DCB,不能添加的条件是( )| A. | ∠ABC=∠DCB | B. | AC=DB | C. | ∠A=∠D | D. | OC=OB |
11.在半径为5cm的⊙O中,圆心O到弦AB的距离为4cm,则弦AB的长为( )
| A. | 3cm | B. | 4cm | C. | 5cm | D. | 6cm |
12. 如图,在△ABC中,BC=6,∠A=90°,∠B=70°.把△ABC沿BC方向平移到△DEF的位置,若CF=2,则下列结论中错误的是( )
如图,在△ABC中,BC=6,∠A=90°,∠B=70°.把△ABC沿BC方向平移到△DEF的位置,若CF=2,则下列结论中错误的是( )
 如图,在△ABC中,BC=6,∠A=90°,∠B=70°.把△ABC沿BC方向平移到△DEF的位置,若CF=2,则下列结论中错误的是( )
如图,在△ABC中,BC=6,∠A=90°,∠B=70°.把△ABC沿BC方向平移到△DEF的位置,若CF=2,则下列结论中错误的是( )| A. | BE=2 | B. | ∠F=20° | C. | AB∥DE | D. | DF=6 |
13. 已知一次函数y=kx+b的图象如图所示,当x<2时,y的取值范围是( )
已知一次函数y=kx+b的图象如图所示,当x<2时,y的取值范围是( )
 已知一次函数y=kx+b的图象如图所示,当x<2时,y的取值范围是( )
已知一次函数y=kx+b的图象如图所示,当x<2时,y的取值范围是( )| A. | y<-4 | B. | -4<y<0 | C. | y<2 | D. | y<0 |
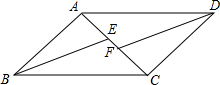 如图,四边形ABCD是平行四边形,BE、DF分别是∠ABC、∠ADC的平分线,且与对角线AC分别相交于点E、F.
如图,四边形ABCD是平行四边形,BE、DF分别是∠ABC、∠ADC的平分线,且与对角线AC分别相交于点E、F.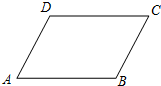 如图,已知四边形ABCD中,AB∥CD,若不添加任何辅助线,请添加一个条件:
如图,已知四边形ABCD中,AB∥CD,若不添加任何辅助线,请添加一个条件: