题目内容
8．若菱形的两条对角线的比为3：4，且周长为20cm，则它的面积等于24cm2．分析 根据菱形的周长即可求菱形的边长，根据对角线的比为3：4，即可求两条对角线的值，根据对角线的长即可计算菱形的面积．
解答 
解：设BO=4x，则AO=3x，
菱形周长为20cm，则AB=5cm，
菱形对角线互相垂直平分，
∴（3x）2+（4x）2=52
得x=1，即AO=3cm，BO=4cm，
∴菱形的面积为S=$\frac{1}{2}$×6cm×8cm=24cm2，
故答案为：24．
点评 本题考查了菱形面积的计算，考查了勾股定理在直角三角形中的运用，本题中根据勾股定理求AO、BO的值是解题的关键．
练习册系列答案
智能训练练测考系列答案
计算高手系列答案
相关题目
18．∠α的余角为65°，则∠α的度数为（ ）
| A． | 35° | B． | 25° | C． | 45° | D． | 65° |
19．
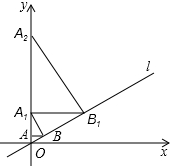如图，直线l为正比例函数y=$\frac{\sqrt{3}}{3}$x的图象，过点A（0，1）作y轴的垂线交直线l于点B，过点B作直线l的垂线交y轴于点A1；过点A1作y轴的垂线交直线l于点B1，过点B1作直线l的垂线交y轴于点A2；…；按此作法继续下去，则点Bn的坐标是（ ）
如图，直线l为正比例函数y=$\frac{\sqrt{3}}{3}$x的图象，过点A（0，1）作y轴的垂线交直线l于点B，过点B作直线l的垂线交y轴于点A1；过点A1作y轴的垂线交直线l于点B1，过点B1作直线l的垂线交y轴于点A2；…；按此作法继续下去，则点Bn的坐标是（ ）| A． | （$\sqrt{3}$×4n，4n） | B． | （$\sqrt{3}$×4n-1，4n-1） | C． | （$\sqrt{3}$×4n-1，4n） | D． | （$\sqrt{3}$×4n，4n-1） |
如图是边长为2的正方形ABCD，对角线为AC，△ABC以点A为中心，顺时针旋转45°得△AB′C′，则图中阴影部分的面积为4$\sqrt{2}$-4．
13．下面给出了四边形ABCD中∠A，∠B，∠C，∠D的度数之比，其中能判定四边形ABCD是平行四边形的是（ ）
| A． | 1：2：3：4 | B． | 2：2：3：3 | C． | 2；3：2：3 | D． | 2：3：3：2 |
20．
已知一块蓄电池的电压为定值，电流I（A）与电阻R（Ω）之间的函数关系如图，则电流I关于电阻R的函数解析式为（ ）
已知一块蓄电池的电压为定值，电流I（A）与电阻R（Ω）之间的函数关系如图，则电流I关于电阻R的函数解析式为（ ）| A． | I=$\frac{32}{R}$ | B． | I=-$\frac{32}{R}$ | C． | I=$\frac{4}{R}$ | D． | I=$\frac{8}{R}$ |
如图，将三角形AOB绕点O逆时针旋转到三角形COD的位置，若旋转角是20°，则∠AOC的度数为20°．