题目内容
13.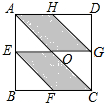 如图,正方形ABCD是一块绿化带,E,F,G,H分别是AB,BC,CD,AD的中点,阴影部分EOCF,AOGH都是花圃,一只自由飞翔的小鸟,将随机落在这块绿化带上,则小鸟在花圃上的概率为( )
如图,正方形ABCD是一块绿化带,E,F,G,H分别是AB,BC,CD,AD的中点,阴影部分EOCF,AOGH都是花圃,一只自由飞翔的小鸟,将随机落在这块绿化带上,则小鸟在花圃上的概率为( )| A. | $\frac{1}{2}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{3}$ | D. | $\frac{2}{5}$ |
分析 用阴影部分的面积除以正方形的面积即可求得小鸟在花圃上的概率.
解答 解:∵正方形ABCD是一块绿化带,E,F,G,H分别是AB,BC,CD,AD的中点,
∴S四边形AHGO+S四边形OEFC=$\frac{1}{2}$S正方形ABCD,
∴一只自由飞翔的小鸟,将随机落在这块绿化带上,则小鸟在花圃上的概率为$\frac{1}{2}$,
故选A.
点评 本题考查了几何概率的知识,解题的关键是求得阴影部分的面积与正方形的面积的比,难度不大.

练习册系列答案
相关题目
8.一个手机经销商计划购进某品牌的A型、B型、C型三款手机共60部,每款手机至少要购进8部,且恰好用完购机款61000元.设购进A型手机x部、B型手机y部,三款手机的进价和预售价如表:
(1)用含x,y的式子表示购进C型手机的部数;
(2)求出y与x之间的函数关系式;
(3)假设所购进手机全部售出,综合考虑各种因素,该手机经销商在购销这批手机过程中需另外支出各种费用共1500元.
①求出预估利润P(元)与x(部)的函数关系式;
(注:预估利润P=预售总额-购机款-各种费用)
②求出预估利润的最大值,并写出此时购进三款手机各多少部.
| 手机型号 | A型 | B型 | C型 |
| 进价(单位:元/部) | 900 | 1200 | 1100 |
| 预售价(单位:元/部) | 1200 | 1600 | 1300 |
(2)求出y与x之间的函数关系式;
(3)假设所购进手机全部售出,综合考虑各种因素,该手机经销商在购销这批手机过程中需另外支出各种费用共1500元.
①求出预估利润P(元)与x(部)的函数关系式;
(注:预估利润P=预售总额-购机款-各种费用)
②求出预估利润的最大值,并写出此时购进三款手机各多少部.
18.∠α的余角为65°,则∠α的度数为( )
| A. | 35° | B. | 25° | C. | 45° | D. | 65° |
2.当a=-1时,分式$\frac{{{a^2}+a}}{{{a^2}-a}}$( )
| A. | 等于零 | B. | 等于1 | C. | 等于-1 | D. | 没有意义 |
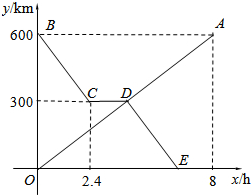 货车和轿车分别从甲、乙两地同时出发,沿同一公路相向而行.轿车出发2.4h后休息,直至与货车相遇后,以原速度继续行驶.设货车出发xh后,货车、轿车分别到达离甲地y1km和y2km的地方,图中的线段OA、折线BCDE分别表示y1、y2与x之间的函数关系.
货车和轿车分别从甲、乙两地同时出发,沿同一公路相向而行.轿车出发2.4h后休息,直至与货车相遇后,以原速度继续行驶.设货车出发xh后,货车、轿车分别到达离甲地y1km和y2km的地方,图中的线段OA、折线BCDE分别表示y1、y2与x之间的函数关系.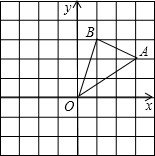 如图,在边长为1的正方形组成的网格中建立直角坐标系,△AOB的顶点均在格点上,点O为原点,点A,B的坐标分别是(3,2)、B(1,3).
如图,在边长为1的正方形组成的网格中建立直角坐标系,△AOB的顶点均在格点上,点O为原点,点A,B的坐标分别是(3,2)、B(1,3).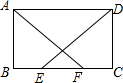 如图,在?ABCD中,E、F为边BC上两点,且BE=CF,AF=DE.
如图,在?ABCD中,E、F为边BC上两点,且BE=CF,AF=DE.