题目内容
13．
已知一次函数y=kx+b的图象如图所示，当x＜2时，y的取值范围是（ ）| A． | y＜-4 | B． | -4＜y＜0 | C． | y＜2 | D． | y＜0 |
分析 由函数图象找出点的坐标，利用待定系数法即可求出函数解析式，再根据函数的性质找出函数的单调性，代入x＜2即可得出结论．
解答 解：将（2，0）、（0，-4）代入y=kx+b中，
得：$\left\{\begin{array}{l}{0=2k+b}\\{-4=b}\end{array}\right.$，解得：$\left\{\begin{array}{l}{k=2}\\{b=-4}\end{array}\right.$，
∴一次函数解析式为y=2x-4．
∵k=2＞0，
∴该函数y值随x值增加而增加，
∴y＜2×2-4=0．
故选D．
点评 本题考查了待定系数法求出函数解析式以及一次函数的性质，解题的关键是找出该一次函数的单调性．本题属于基础题，难度不大，解决该题型题目时，根据函数图象找出点的坐标，利用待定系数法求出函数解析式是关键．
练习册系列答案
学业测评一课一测系列答案
相关题目
1．某品牌手机，去年每台的售价y（元）与月份x之间满足关系y=-50x+2600，去年的月销量p（万元）与月份x之间成一次函数关系，其中第一季度的销量情况如表：
（1）求p关于x的函数关系式；
（2）求去年12月份的销售量与销售价格；
（3）今年1月份比去年12月份该品牌手机的售价下降的百分率为m，销售量下降的百分率为1.5m，今年2月份，经销商对该手机以1月份价格的八折销售，这样2月份的销售量比今年1月份增加了1.5万台，销售额为6400万元，求m的值．
| 月份（x） | 1月 | 2月 | 3月 |
| 销售量（p） | 3.9万台 | 4.0万台 | 4.1万台 |
（2）求去年12月份的销售量与销售价格；
（3）今年1月份比去年12月份该品牌手机的售价下降的百分率为m，销售量下降的百分率为1.5m，今年2月份，经销商对该手机以1月份价格的八折销售，这样2月份的销售量比今年1月份增加了1.5万台，销售额为6400万元，求m的值．
8．已知在平面直角坐标系中，点A的坐标为（3，0），点B的坐标为（0，4），连接AB，现将线段AB进行平移，平移后得到点B的对应点D的坐标为（1，5），则点A的对应点C的坐标为（ ）
| A． | （3，0） | B． | （4，1） | C． | （2，-1） | D． | （0，5） |
如图，将三角形AOB绕点O逆时针旋转到三角形COD的位置，若旋转角是20°，则∠AOC的度数为20°．
5．某校举行“汉字听写”比赛，每位学生听写汉字39个，比赛结束后随机抽查部分学生的听写结果，以下是根据 抽查结果绘制的统计图的一部分．
根据以上信息解决下列问题：
（1）该次随机抽查的样本容量是200．
（2）在统计表中，m=60，n=40．
（3）补全条形统计图．
（4）扇形统计图中“C组”所对应的圆心角的度数是90°．
| 组别 | 正确字数x | 人数 |
| A | 0≤x＜8 | 20 |
| B | 8≤x＜16 | 30 |
| C | 16≤x＜24 | 50 |
| D | 24≤x＜32 | m |
| E | 32≤x＜40 | n |
（1）该次随机抽查的样本容量是200．
（2）在统计表中，m=60，n=40．
（3）补全条形统计图．
（4）扇形统计图中“C组”所对应的圆心角的度数是90°．
如图，点A、点B分别是反比例函数y=$\frac{4}{x}$和反比例函数y=$\frac{2}{x}$的图象上的点，且AB∥y轴，连接OA、OB，则△AOB的面积为1．
3．
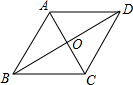如图，在菱形ABCD中，对角线AC与BD相交于点O，若AB=2，∠ABC=60°，则BD的长为（ ）
如图，在菱形ABCD中，对角线AC与BD相交于点O，若AB=2，∠ABC=60°，则BD的长为（ ）| A． | 2 | B． | 3 | C． | $\sqrt{3}$ | D． | 2$\sqrt{3}$ |