题目内容
7.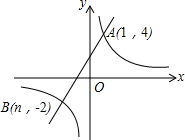 如图,已知反比例函数y=$\frac{m}{x}$的图象与一次函数y=ax+b的图象相交于点A(1,4)和点B(n,-2).
如图,已知反比例函数y=$\frac{m}{x}$的图象与一次函数y=ax+b的图象相交于点A(1,4)和点B(n,-2).(1)求反比例函数和一次函数的解析式;
(2)写出在第一象限内当一次函数的值大于反比例函数的值时x的取值范围.
分析 (1)把A的坐标代入反比例函数的解析式,求出m的值,从而确定反比例函数的解析式,把B的坐标代入反比例函数解析式求出B的坐标,把A、B的坐标代入一次函数的解析式,即可求出a,b的值,从而确定一次函数的解析式;
(2)根据函数的图象即可得出一次函数的值小于反比例函数的值的x的取值范围.
解答 解:(1)∵反比例函数y=$\frac{m}{x}$的图象经过点A(1,4),
∴m=1×4=4,
反比例函数的解析式为y=$\frac{4}{m}$;
∵反比例函数y=$\frac{4}{m}$的图象经过点B(n,-2),
∴-2n=4,∴n=-2,
∴B(-2,-2).
∵一次函数y=ax+b的图象经过点A(1,4)、B(-2,-2),
∴$\left\{\begin{array}{l}{a+b=4}\\{-2a+b=-2}\end{array}\right.$,解得$\left\{\begin{array}{l}{a=2}\\{b=2}\end{array}\right.$,
∴一次函数的解析式为y=2x+2;
(2)当x>1时,在第一象限内一次函数的值大于反比例函数的值.
点评 本题考查了一次函数与反比例函数的交点问题,用待定系数法求一次函数和反比例函数的解析式及利用图象比较函数值的大小.解题的关键是:确定交点的坐标.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
18.(x-2)(x+3)的运算的结果是( )
| A. | x2-6 | B. | x2+6 | C. | x2-5x-6 | D. | x2+x-6 |
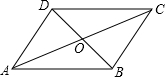 如图,在平行四边形ABCD中,O是对角线AC,BD的交点
如图,在平行四边形ABCD中,O是对角线AC,BD的交点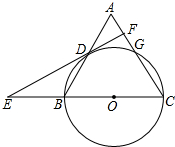 如图,在△ABC中,CA=CB,以BC为直径的圆⊙O交AC于点G,交AB于点D,过点D作⊙O的切线,交CB的延长线于点E,交AC于点F.
如图,在△ABC中,CA=CB,以BC为直径的圆⊙O交AC于点G,交AB于点D,过点D作⊙O的切线,交CB的延长线于点E,交AC于点F.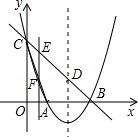 如图.抛物线y=x2+bx+c与y轴交于点C(0,3),与x轴交于A,B两点,A点在对称轴的左侧,B点的坐标为(3,0).
如图.抛物线y=x2+bx+c与y轴交于点C(0,3),与x轴交于A,B两点,A点在对称轴的左侧,B点的坐标为(3,0).