Question

15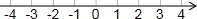．（1）计算：$\sqrt{12}+（-\frac{1}{2}）^{-1}$-2tan60°-（-1）²⁰¹⁵；
（2）解不等式组$\left\{\begin{array}{l}{5x-1＞3x-4}\\{\frac{2}{3}-x≥-\frac{1}{3}}\end{array}\right.$，并把不等式组的解集在数轴上表示出来．

Answer 1

分析 （1）原式第一项化为最简二次根式，第二项利用负整数指数幂法则计算，第三项利用特殊角的三角函数值计算，最后一项利用乘方的意义计算即可得到结果；
（2）分别求出不等式组中两不等式的解集，找出解集的公共部分即可．

解答 解：（1）原式=2$\sqrt{3}$-2-2$\sqrt{3}$+1=-1；
（2）$\left\{\begin{array}{l}{5x-1＞3x-4①}\\{\frac{2}{3}-x≥-\frac{1}{3}②}\end{array}\right.$，
由①得：x＞-$\frac{3}{2}$；
由②得：x≤1，
则不等式组的解集为-$\frac{3}{2}$＜x≤1，

点评 此题考查了实数的运算，熟练掌握运算法则是解本题的关键．