题目内容
6.已知直角坐标系中菱形ABCD的位置如图,C,D两点的坐标分别为(4,0),(0,3)现有两动点P,Q分别从A,C同时出发,点P沿线段AD向终点D运动,速度为1个单位/s,点Q沿折线CBA向终点A运动,速度为2个单位/s,设运动时间为t s.(1)求AD与BC间的距离h;
(2)若四边形PQCD为平行四边形,求t的值;
(3)是否存在某一时刻,使得P,Q两点同时在反比例函数y=$\frac{k}{x}$的图象上?若存在,求出此时t与k的值.

分析 (1)根据菱形的面积等于对角线乘积的一半求出面积,求出AD与BC间的距离h;
(2)根据对边平行且相等的四边形是平行四边形解得即可;
(3)根据相似三角形的性质用t表示出点Q和点P的坐标,根据反比例函数的系数的意义即k=xy计算即可.
解答 解:(1)∵C,D两点的坐标分别为(4,0),(0,3),
∴OC=4,OD=3,
∴CD=5,
由菱形的面积公式可以得到,5×h=$\frac{1}{2}$×3×4×4,
解得,h=4.8;
(2)当点Q在BC上时,PD=CQ,四边形PQCD为平行四边形,
即5-t=2t,
解得,t=$\frac{5}{3}$;
当点Q在AB上时,四边形PQCD不能为平行四边形,
∴t=$\frac{5}{3}$时,四边形PQCD为平行四边形;
(3) 当点Q在在BC上时,作QF⊥AC于F,PE⊥AC于E,
当点Q在在BC上时,作QF⊥AC于F,PE⊥AC于E,
由题意得,AP=t,CQ=2t,
∵PE∥OD,
∴$\frac{PE}{OD}$=$\frac{AP}{AD}$=$\frac{AE}{OA}$,即$\frac{PE}{3}$=$\frac{t}{5}$=$\frac{AE}{4}$,
解得,PE=$\frac{3}{5}$t,AE=$\frac{4}{5}$t,
则OE=4-$\frac{4}{5}$t,
∴点P的坐标为($\frac{4}{5}$t-4,$\frac{3}{5}$t),
∵FQ∥OB,
∴$\frac{QF}{OB}$=$\frac{CF}{OC}$=$\frac{CQ}{CB}$,即$\frac{QF}{3}$=$\frac{2t}{5}$=$\frac{CF}{4}$,
解得,QF=$\frac{6}{5}$t,CF=$\frac{8}{5}$t,
则OF=4-$\frac{8}{5}$t,
∴点Q的坐标为(4-$\frac{8}{5}$t,-$\frac{6}{5}$t),
∵P,Q两点同时在反比例函数y=$\frac{k}{x}$的图象上,
∴($\frac{4}{5}$t-4)×$\frac{3}{5}$t=(4-$\frac{8}{5}$t)×(-$\frac{6}{5}$t),
解得,t1=0(舍去),t2=$\frac{5}{3}$,
当t=$\frac{5}{3}$时,k=($\frac{4}{5}$t-4)×$\frac{3}{5}$t=-$\frac{8}{3}$,
当点Q在AB上时,点P在第二象限,点Q在第三象限,P,Q两点不可能同时在反比例函数y=$\frac{k}{x}$的图象上,
∴P,Q两点同时在反比例函数y=$\frac{k}{x}$的图象上时,t=$\frac{5}{3}$,k=-$\frac{8}{3}$.
点评 本题考查的是反比例函数的综合运用、菱形的性质、相似三角形的性质,掌握反比例函数的系数k的意义、灵活运用相似三角形的判定定理和性质定理是解题的关键,注意分情况讨论思想的应用.

 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案| A. | 与x轴有两个交点 | B. | 开口向上 | ||
| C. | 与y轴的交点坐标是(0,3) | D. | 当x=1时,y有最大值为-2 |
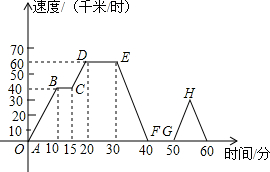 星期天到外婆家去,他记录了汽车行驶的速度随时间的变化情况,到了外婆家画出如图所示的图象
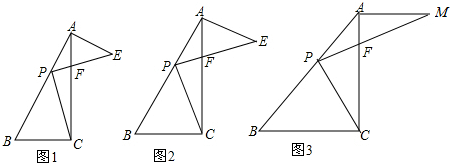
星期天到外婆家去,他记录了汽车行驶的速度随时间的变化情况,到了外婆家画出如图所示的图象 如图,在Rt△AGD中,以斜边AD为边在△AGD外作正方形ABCD,连接CG,BG,已知AG=DG=1.
如图,在Rt△AGD中,以斜边AD为边在△AGD外作正方形ABCD,连接CG,BG,已知AG=DG=1. (1)计算:$\sqrt{12}+(-\frac{1}{2})^{-1}$-2tan60°-(-1)2015;
(1)计算:$\sqrt{12}+(-\frac{1}{2})^{-1}$-2tan60°-(-1)2015;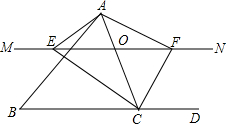 如图,在△ABC中,点O是AC边上的一动点,过点O作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F.
如图,在△ABC中,点O是AC边上的一动点,过点O作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F.