题目内容
7.方程$\frac{1}{x-2}$-$\frac{1}{x-4}$=$\frac{1}{x-3}$-$\frac{1}{x-5}$的解是x=$\frac{7}{2}$;方程$\frac{1}{x-7}$-$\frac{1}{x-5}$=$\frac{1}{x-6}$-$\frac{1}{x-4}$的解是x=$\frac{11}{2}$.
(1)试猜想方程$\frac{1}{x-7}$+$\frac{1}{x-1}$=$\frac{1}{x-6}$$+\frac{1}{x-2}$的解;
(2)验证(1)的解并猜想方程$\frac{1}{x-a}$-$\frac{1}{x-b}$=$\frac{1}{x-c}$$-\frac{1}{x-d}$的解.(a,b,c,d表示不同的数,且a+d=b+c)
分析 (1))首先把$\frac{1}{x-7}$+$\frac{1}{x-1}$=$\frac{1}{x-6}$$+\frac{1}{x-2}$转化成$\frac{1}{x-1}$-$\frac{1}{x-2}$=$\frac{1}{x-6}$-$\frac{1}{x-7}$,然后根据方程$\frac{1}{x-2}$-$\frac{1}{x-4}$=$\frac{1}{x-3}$-$\frac{1}{x-5}$的解是x=$\frac{7}{2}$=$\frac{2+5}{2}$;方程$\frac{1}{x-7}$-$\frac{1}{x-5}$=$\frac{1}{x-6}$-$\frac{1}{x-4}$的解是x=$\frac{11}{2}$=$\frac{7+4}{2}$;猜想方程$\frac{1}{x-7}$+$\frac{1}{x-1}$=$\frac{1}{x-6}$$+\frac{1}{x-2}$的解是多少即可.
(2)首先验证x=4是方程$\frac{1}{x-7}$+$\frac{1}{x-1}$=$\frac{1}{x-6}$$+\frac{1}{x-2}$的解;然后根据a+d=b+c,猜想方程$\frac{1}{x-a}$-$\frac{1}{x-b}$=$\frac{1}{x-c}$$-\frac{1}{x-d}$的解是x=$\frac{a+d}{2}$.
解答 解:(1)∵$\frac{1}{x-7}$+$\frac{1}{x-1}$=$\frac{1}{x-6}$$+\frac{1}{x-2}$,
∴$\frac{1}{x-1}$-$\frac{1}{x-2}$=$\frac{1}{x-6}$-$\frac{1}{x-7}$,
∵方程$\frac{1}{x-2}$-$\frac{1}{x-4}$=$\frac{1}{x-3}$-$\frac{1}{x-5}$的解是x=$\frac{7}{2}$=$\frac{2+5}{2}$;
方程$\frac{1}{x-7}$-$\frac{1}{x-5}$=$\frac{1}{x-6}$-$\frac{1}{x-4}$的解是x=$\frac{11}{2}$=$\frac{7+4}{2}$;
∴猜想方程$\frac{1}{x-7}$+$\frac{1}{x-1}$=$\frac{1}{x-6}$$+\frac{1}{x-2}$的解是x=$\frac{1+7}{2}$=4.
(2)当x=4时,
∵$\frac{1}{x-7}$+$\frac{1}{x-1}$=$\frac{1}{4-7}+\frac{1}{4-1}=-\frac{1}{3}+\frac{1}{3}=0$
$\frac{1}{x-6}$$+\frac{1}{x-2}$=$\frac{1}{4-6}+\frac{1}{4-2}=-\frac{1}{2}+\frac{1}{2}=0$,
∴方程$\frac{1}{x-7}$+$\frac{1}{x-1}$=$\frac{1}{x-6}$$+\frac{1}{x-2}$的解是x=4.
∵a+d=b+c,
∴猜想方程$\frac{1}{x-a}$-$\frac{1}{x-b}$=$\frac{1}{x-c}$$-\frac{1}{x-d}$的解是x=$\frac{a+d}{2}$(或x=$\frac{b+c}{2}$).
点评 此题主要考查了形如$\frac{1}{x-a}$-$\frac{1}{x-b}$=$\frac{1}{x-c}$$-\frac{1}{x-d}$的分式方程的解,要注意观察总结出规律,并能正确的应用规律.

 如图,AB=AC=AD,BE⊥BC,DE⊥CD,若∠BAD=100°,则∠E=( )
如图,AB=AC=AD,BE⊥BC,DE⊥CD,若∠BAD=100°,则∠E=( )| A. | 45° | B. | 50° | C. | 55° | D. | 60° |
 如图,在Rt△AGD中,以斜边AD为边在△AGD外作正方形ABCD,连接CG,BG,已知AG=DG=1.
如图,在Rt△AGD中,以斜边AD为边在△AGD外作正方形ABCD,连接CG,BG,已知AG=DG=1. (1)计算:$\sqrt{12}+(-\frac{1}{2})^{-1}$-2tan60°-(-1)2015;
(1)计算:$\sqrt{12}+(-\frac{1}{2})^{-1}$-2tan60°-(-1)2015;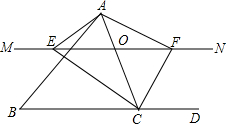 如图,在△ABC中,点O是AC边上的一动点,过点O作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F.
如图,在△ABC中,点O是AC边上的一动点,过点O作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F.