题目内容
10.若y=x2+bx+c的图象与x轴两个交点间的距离为4,图象经过点(2,-3),则此二次函数的解析式为y=x2-2x-3或y=x2-6x+5.分析 根据交点和系数的关系得出x1+x2=-b,x1x2=c,根据|x1-x2|=4,得出b2-4c=16,把点(2,-3)代入解析式得出4+2b+c=-3,解$\left\{\begin{array}{l}{{b}^{2}-4c=16}\\{c=-7-2b}\end{array}\right.$即可求得系数b、c.
解答 解:设抛物线与x轴的交点坐标为(x1,0),(x2,0),
根据题意得:x1+x2=-b,x1x2=c,
∵|x1-x2|=4,
∴(x1-x2)2=(x1+x2)2-4x1x2=16,
整理得:b2-4c=16①,
把(2,-3)代入得:4+2b+c=-3②,
联立①②得:$\left\{\begin{array}{l}{{b}^{2}-4c=16}\\{c=-7-2b}\end{array}\right.$,
解得$\left\{\begin{array}{l}{{b}_{1}=-2}\\{{c}_{1}=-3}\end{array}\right.$,$\left\{\begin{array}{l}{{b}_{2}=-6}\\{{c}_{2}=5}\end{array}\right.$,
∴此二次函数的解析式为y=x2-2x-3或y=x2-6x+5.
故答案为y=x2-2x-3或y=x2-6x+5.
点评 本题考查了待定系数法求二次函数的解析式,应用交点和系数的关系求得系数的值是解题的关键.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案
相关题目
2. 如图,AB=AC=AD,BE⊥BC,DE⊥CD,若∠BAD=100°,则∠E=( )
如图,AB=AC=AD,BE⊥BC,DE⊥CD,若∠BAD=100°,则∠E=( )
 如图,AB=AC=AD,BE⊥BC,DE⊥CD,若∠BAD=100°,则∠E=( )
如图,AB=AC=AD,BE⊥BC,DE⊥CD,若∠BAD=100°,则∠E=( )| A. | 45° | B. | 50° | C. | 55° | D. | 60° |
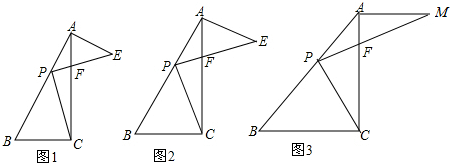
 如图,在Rt△AGD中,以斜边AD为边在△AGD外作正方形ABCD,连接CG,BG,已知AG=DG=1.
如图,在Rt△AGD中,以斜边AD为边在△AGD外作正方形ABCD,连接CG,BG,已知AG=DG=1.
 (1)计算:$\sqrt{12}+(-\frac{1}{2})^{-1}$-2tan60°-(-1)2015;
(1)计算:$\sqrt{12}+(-\frac{1}{2})^{-1}$-2tan60°-(-1)2015;