题目内容
15.阅读下列文字与例题:将一个多项式分组后,可提公因式或运用公式继续分解的方法称作分组分解.
例如:以下两个式子的分解因式的方法就称为分组分解法.
(1)am+an+bm+bn=(am+bm)+(an+bn)=m(a+b)+n(a+b)=(a+b)(m+n);
(2)x2-y2-2y-1=x2-(y2+2y+1)=x2-(y+1)2=(x+y+1)(x+y-1)
试用上述方法分解因式:
(1)a2+2ab+b2+ac+bc;
(2)4a2-x2+4xy-4y2.
分析 (1)原式前三项结合,后两项结合,利用完全平方公式及提取公因式方法分解即可;
(2)原式后三项提取-1,利用完全平方公式及平方差公式分解即可.
解答 解:(1)原式=(a2+2ab+b2)+(ac+bc)=(a+b)2+c(a+b)=(a+b)(a+b+c);
(2)原式=4a2-(x2-4xy+4y2)=4a2-(x-2y)2=(2a+x-2y)(2a-x+2y).
点评 此题考查了分解因式-十字相乘法,以及分组分解法,熟练掌握因式分解的方法是解本题的关键.

练习册系列答案
相关题目
5.|-8|的相反数是( )
| A. | -8 | B. | 8 | C. | $\frac{1}{8}$ | D. | -$\frac{1}{8}$ |
6. 如图所示,$\frac{AD}{AE}$=$\frac{AC}{AB}$=$\frac{1}{3}$,则下列结论不成立的是( )
如图所示,$\frac{AD}{AE}$=$\frac{AC}{AB}$=$\frac{1}{3}$,则下列结论不成立的是( )
 如图所示,$\frac{AD}{AE}$=$\frac{AC}{AB}$=$\frac{1}{3}$,则下列结论不成立的是( )
如图所示,$\frac{AD}{AE}$=$\frac{AC}{AB}$=$\frac{1}{3}$,则下列结论不成立的是( )| A. | △ABE∽△ACD | B. | △BOD∽△COE | C. | OC=OD | D. | CD:BE=1:3 |
4.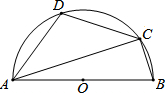 如图,AB为半圆O的直径,C、D是半圆上的两点,且D是$\widehat{AC}$的中点,连接AC,若∠B=70°,则∠DAB的度数为( )
如图,AB为半圆O的直径,C、D是半圆上的两点,且D是$\widehat{AC}$的中点,连接AC,若∠B=70°,则∠DAB的度数为( )
 如图,AB为半圆O的直径,C、D是半圆上的两点,且D是$\widehat{AC}$的中点,连接AC,若∠B=70°,则∠DAB的度数为( )
如图,AB为半圆O的直径,C、D是半圆上的两点,且D是$\widehat{AC}$的中点,连接AC,若∠B=70°,则∠DAB的度数为( )| A. | 54° | B. | 55° | C. | 56° | D. | 57° |
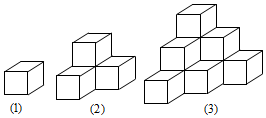 用棱长为1的小正方体按照如图所示的摆放规律,逐个排成若干个无缝隙的几何体,图1几何体表面积为6,图2几何体表面积为18.
用棱长为1的小正方体按照如图所示的摆放规律,逐个排成若干个无缝隙的几何体,图1几何体表面积为6,图2几何体表面积为18. 如图,在6×8的网格图中,每个小正方形边长均为1,原点O和△ABC的顶点均为格点.
如图,在6×8的网格图中,每个小正方形边长均为1,原点O和△ABC的顶点均为格点.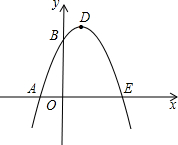 如图,已知抛物线与x轴交于A(-1,0)、E(3,0)两点,与y轴交于点B(0,3).
如图,已知抛物线与x轴交于A(-1,0)、E(3,0)两点,与y轴交于点B(0,3).