题目内容
3.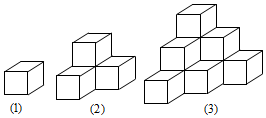 用棱长为1的小正方体按照如图所示的摆放规律,逐个排成若干个无缝隙的几何体,图1几何体表面积为6,图2几何体表面积为18.
用棱长为1的小正方体按照如图所示的摆放规律,逐个排成若干个无缝隙的几何体,图1几何体表面积为6,图2几何体表面积为18.(1)图3几何体的表面积为36;
(2)图67几何体的表面积为13668.
分析 根据已知图形的面积得出变化规律,第n个几何体的表面积为:3n(n+1),进而求出答案.
解答  解:(1)第①个几何体的表面积为:6=3×1×(1+1),
解:(1)第①个几何体的表面积为:6=3×1×(1+1),
第②个几何体的表面积为18=3×2×(2+1),
故第③个几何体的表面积为3×3×(3+1)=36,
故答案为:36;
(2)第④个几何体的表面积为3×4(4+1)=60,…,
按照这样的规律,第n个几何体的表面积为:3n(n+1),
∴第67个几何体的表面积为3×67×68=13668.
故答案为:13668.
点评 此题主要考查了几何体的表面积以及图形的变化规律,根据图形面积得出数字之间的变化规律是解题关键.

练习册系列答案
相关题目
13.从5点15分到5点20分,分针旋转的度数为( )
| A. | 20° | B. | 26° | C. | 30° | D. | 36° |
14.下列命题错误的是( )
| A. | 经过三个点一定可以作圆 | |
| B. | 三角形的外心到三角形各顶点的距离相等 | |
| C. | 同圆中,相等的圆心角所对的弧相等 | |
| D. | 经过切点且垂直于切线的直线必经过圆心 |
8.下列二次根式中,最简二次根式为( )
| A. | $\sqrt{\frac{1}{3}}$ | B. | $\sqrt{6}$ | C. | $\sqrt{9}$ | D. | $\sqrt{18}$ |

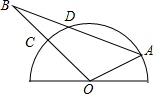 如图,半圆O是一个量角器,△AOB为一纸片,AB交半圆于点D,OB交半圆于点C,若点C、D、A在量角器上对应读数分别为45°,70°,150°,则∠AOB的度数为105°;∠A的度数为50°.
如图,半圆O是一个量角器,△AOB为一纸片,AB交半圆于点D,OB交半圆于点C,若点C、D、A在量角器上对应读数分别为45°,70°,150°,则∠AOB的度数为105°;∠A的度数为50°.