题目内容
7.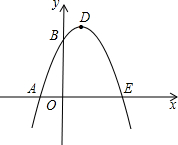 如图,已知抛物线与x轴交于A(-1,0)、E(3,0)两点,与y轴交于点B(0,3).
如图,已知抛物线与x轴交于A(-1,0)、E(3,0)两点,与y轴交于点B(0,3).(1)求抛物线的解析式;
(2)求抛物线顶点D的坐标,及对称轴;
(3)根据图象回答当:当x为何值时,函数值大于0.
分析 (1)待定系数法求解可得;
(2)配方成顶点式可得;
(3)由函数图象位于x轴上方的部分对应的x的范围可得.
解答 解:(1)设抛物线的解析式为y=a(x+1)(x-3),
将点B(0,3)代入,得:-3a=3,
解得:a=-1,
∴抛物线解析式为y=-(x+1)(x-3)=-x2+2x+3;
(2)∵y=-x2+2x+3=-(x-1)2+4,
∴抛物线的顶点D的坐标为(1,4),对称轴为直线x=1;
(3)由图象知,当-1<x<3时,抛物线位于x轴上方,
∴当-1<x<3时,函数值大于0.
点评 本题主要考查待定系数法求函数解析式及抛物线与x轴的交点,熟练掌握抛物线求函数解析式及二次函数的性质、二次函数与一元二次不等式间的关系是解题的关键.

练习册系列答案
相关题目
17.小明沿着坡角为40°的坡面向下走了m米,那么他下降( )米.
| A. | msin40° | B. | mcos40° | C. | mtan40° | D. | $\frac{m}{tan40°}$ |

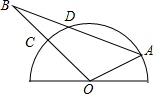 如图,半圆O是一个量角器,△AOB为一纸片,AB交半圆于点D,OB交半圆于点C,若点C、D、A在量角器上对应读数分别为45°,70°,150°,则∠AOB的度数为105°;∠A的度数为50°.
如图,半圆O是一个量角器,△AOB为一纸片,AB交半圆于点D,OB交半圆于点C,若点C、D、A在量角器上对应读数分别为45°,70°,150°,则∠AOB的度数为105°;∠A的度数为50°.