题目内容
4.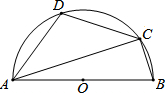 如图,AB为半圆O的直径,C、D是半圆上的两点,且D是$\widehat{AC}$的中点,连接AC,若∠B=70°,则∠DAB的度数为( )
如图,AB为半圆O的直径,C、D是半圆上的两点,且D是$\widehat{AC}$的中点,连接AC,若∠B=70°,则∠DAB的度数为( )| A. | 54° | B. | 55° | C. | 56° | D. | 57° |
分析 连接BD,如图,利用圆周角定理得到∠ABD=∠CBD=$\frac{1}{2}∠$ABC═35°,∠ADB=90°,然后利用互余计算∠DAB的度数.
解答 解:连接BD,如图,
∵D是$\widehat{AC}$的中点,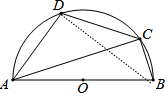
∴$\widehat{AD}$=$\widehat{CD}$,
∴∠ABD=∠CBD=$\frac{1}{2}∠$ABC=$\frac{1}{2}$×70°=35°,
∵AB为直角,
∴∠ADB=90°,
∴∠DAB=90°-∠ABD=90°-35°=55°.
故选B.
点评 本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.推论:半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.

练习册系列答案
相关题目
14.下列命题错误的是( )
| A. | 经过三个点一定可以作圆 | |
| B. | 三角形的外心到三角形各顶点的距离相等 | |
| C. | 同圆中,相等的圆心角所对的弧相等 | |
| D. | 经过切点且垂直于切线的直线必经过圆心 |
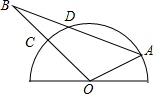 如图,半圆O是一个量角器,△AOB为一纸片,AB交半圆于点D,OB交半圆于点C,若点C、D、A在量角器上对应读数分别为45°,70°,150°,则∠AOB的度数为105°;∠A的度数为50°.
如图,半圆O是一个量角器,△AOB为一纸片,AB交半圆于点D,OB交半圆于点C,若点C、D、A在量角器上对应读数分别为45°,70°,150°,则∠AOB的度数为105°;∠A的度数为50°. 如图,已知AB=AC,DE垂直平分AB交AB、AC于D、E两点,若AB=12cm,BC=8cm,则△BCE的周长为20cm.
如图,已知AB=AC,DE垂直平分AB交AB、AC于D、E两点,若AB=12cm,BC=8cm,则△BCE的周长为20cm.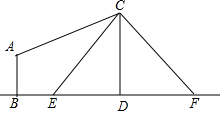 如图,电线杆CD上的C处引拉线CE,CF固定电线杆,在离电线杆6米的B处安置测角仪(点B,E,D在同一直线上),在A处测得电线杆上C处的仰角为30°,已知测角仪的高AB=1.5米,BE=2.3米,求拉线CE的长,(精确到0.1米)参考数据$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73.
如图,电线杆CD上的C处引拉线CE,CF固定电线杆,在离电线杆6米的B处安置测角仪(点B,E,D在同一直线上),在A处测得电线杆上C处的仰角为30°,已知测角仪的高AB=1.5米,BE=2.3米,求拉线CE的长,(精确到0.1米)参考数据$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73.