题目内容
10. 如图,在6×8的网格图中,每个小正方形边长均为1,原点O和△ABC的顶点均为格点.
如图,在6×8的网格图中,每个小正方形边长均为1,原点O和△ABC的顶点均为格点.(1)以O为位似中心,在网格图中作△A′B′C′,使△A′B′C′与
△ABC位似,且位似比为1:2;(保留作图痕迹,不要求写作法和证明)
(2)若点C的坐标为(2,4),
则点A′的坐标为(-1,0),
点C′的坐标为(1,2),
S△A′B′C′:S△ABC=1:4.
分析 (1)利用位似图形的性质得出A′,B′,C′的位置,进而得出答案;
(2)由(1)中所画图形可得.
解答 解:(1)如图,△A′B′C′即为所求作三角形,
(2)由(1)知,A′(-1,0),C′(1,2),
∵位似比为1:2,
∴S△A′B′C′:S△ABC=($\frac{1}{2}$)2=$\frac{1}{4}$,
故答案为:-1,0;1,2;1:4.
点评 此题主要考查了相似变换以及位似变换,利用位似比得出对应点的位置是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目


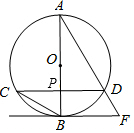 如图,AB为⊙O的直径,弦CD⊥AB,垂足为点P,直线BF与AD延长线交于点F,且∠AFB=∠ABC.
如图,AB为⊙O的直径,弦CD⊥AB,垂足为点P,直线BF与AD延长线交于点F,且∠AFB=∠ABC.