题目内容
2.(1)化简并求值:($\frac{a+3}{{a}^{2}-3a}$$-\frac{a-1}{{a}^{2}-6a+9}$)÷$\frac{a-9}{a}$,其中,a=4.(2)解分式方程:$\frac{1}{x+1}$$-\frac{2}{x-4}$=0.
分析 (1)原式去括号合并得到最简结果,把a的值代入计算即可求出值;
(2)首先方程的两边同乘以最简公分母(x+1)(x-4),把分式方程转化为整式方程,再求解即可,最后要把求得的x的值代入到最简公分母进行检验.
解答 解:(1)原式=[$\frac{a+3}{a(a-3)}$-$\frac{a-1}{(a-3)^{2}}$]÷$\frac{a-9}{a}$
=$\frac{(a+3)(a-3)-a(a-1)}{a(a-3)^{2}}$•$\frac{a}{a-9}$
=$\frac{a-9}{a(a-3)^{2}}$•$\frac{a}{a-9}$
=$\frac{1}{(a-3)^{2}}$,
当a=4时,原式=1;
(2)解:方程两边同乘以(x+1)(x-4)得,(x-4)-2(x+1)=0,
解得:x=-6,
经检验,x=-6是原方程的解.
点评 此题考查了整式的加减-化简求值,解分式方程,关键在于“转化思想”,把分式方程转化为整式方程求解,最后一定注意要验根.熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
10.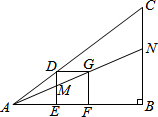 如图△ABC中有一正方形DEFG,其中D在AC上,E、F在AB上,直线AG分别交DE、BC于M、N两点.若∠B=90°,AC=5,BC=3,DG=1,则BN的长度为( )
如图△ABC中有一正方形DEFG,其中D在AC上,E、F在AB上,直线AG分别交DE、BC于M、N两点.若∠B=90°,AC=5,BC=3,DG=1,则BN的长度为( )
 如图△ABC中有一正方形DEFG,其中D在AC上,E、F在AB上,直线AG分别交DE、BC于M、N两点.若∠B=90°,AC=5,BC=3,DG=1,则BN的长度为( )
如图△ABC中有一正方形DEFG,其中D在AC上,E、F在AB上,直线AG分别交DE、BC于M、N两点.若∠B=90°,AC=5,BC=3,DG=1,则BN的长度为( )| A. | $\frac{4}{3}$ | B. | $\frac{3}{2}$ | C. | $\frac{8}{5}$ | D. | $\frac{12}{7}$ |
7.已知m是方程x2-x-2=0的一个根,则代数式m2-m+3=( )
| A. | -2 | B. | 1 | C. | 0 | D. | 5 |
11.当△ABC和△DEF具备( )条件时,△ABC≌△DEF.
| A. | 所有的角对应相等 | B. | 三条边对应相等 | ||
| C. | 面积相等 | D. | 周长相等 |
 已知:⊙O上一点A,作⊙O的内接三角形ABC,使得△ABC为等边三角形.
已知:⊙O上一点A,作⊙O的内接三角形ABC,使得△ABC为等边三角形. 在直角△ABC中,∠C=90°,AC=30cm,BC=40cm.动点M从点C出发,以2cm/s的速度从C向B运动.设点M的运动时间为t(单位:秒).
在直角△ABC中,∠C=90°,AC=30cm,BC=40cm.动点M从点C出发,以2cm/s的速度从C向B运动.设点M的运动时间为t(单位:秒).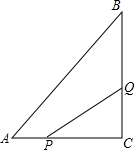 如图所示,在△ABC中,在△ABC中,∠C=90°,AC=6cm,BC=8cm,点P从点A出发沿边AC向点C以1cm/s的速度移动,点Q从C点出发沿CB边向点B以2cm/s的速度移动.
如图所示,在△ABC中,在△ABC中,∠C=90°,AC=6cm,BC=8cm,点P从点A出发沿边AC向点C以1cm/s的速度移动,点Q从C点出发沿CB边向点B以2cm/s的速度移动.