题目内容
17.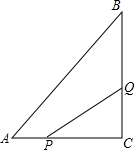 如图所示,在△ABC中,在△ABC中,∠C=90°,AC=6cm,BC=8cm,点P从点A出发沿边AC向点C以1cm/s的速度移动,点Q从C点出发沿CB边向点B以2cm/s的速度移动.
如图所示,在△ABC中,在△ABC中,∠C=90°,AC=6cm,BC=8cm,点P从点A出发沿边AC向点C以1cm/s的速度移动,点Q从C点出发沿CB边向点B以2cm/s的速度移动.(1)如果P、Q同时出发,几秒钟后,可使△PCQ的面积为8cm2?
(2)如果P、Q同时出发,经过几秒钟后,可使△PCQ与△ABC相似?
分析 (1)先用含t的式子表示出PC、QC的长,然后依据三角形的面积公式列方程求解即可;
(2)依据相似三角形对应边成比例列方程求解即可.
解答 解:(1)设t秒后△PCQ的面积为8cm2,则PC=6-t,QC=2t.
根据题意得:$\frac{1}{2}$×2t×(6-t)=8,解得:t=2或t=4.
所以P、Q同时出发,2秒或4秒钟后,可使△PCQ的面积为8cm2.
(2)t秒后PC=6-t,QC=2t.
当△△PCQ∽△ACB时,$\frac{PC}{AC}=\frac{QC}{BC}$,即$\frac{6-t}{6}=\frac{2t}{8}$,解得:t=2.4.
当△PCQ∽△BCA时,$\frac{PC}{BC}=\frac{QC}{AC}$,即$\frac{6-t}{8}=\frac{2t}{6}$,解得:t=$\frac{18}{11}$.
所以当t=2.4或t=$\frac{18}{11}$时,两三角形相似.
点评 本题主要考查的是相似三角形的性质,三角形的面积公式,依据题意列出方程是解题的关键.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案
相关题目
12.下列调查中,最适合采用全面调查(普查)的是( )
| A. | 对肥城市居民日平均用水量的调查 | |
| B. | 对一批LED节能灯使用寿命的调查 | |
| C. | 对肥城新闻栏目收视率的调查 | |
| D. | 对某校七年级(7)班同学身高情况的调查 |
9.若x1,x2是一元二次方程x2-3x+1=0的两个根,则x1+x2=( )
| A. | -3 | B. | 3 | C. | -6 | D. | 6 |
6.如图将4个长、宽分别为a,b的长方形,摆成了一个大的正方形,利用面积的不同表示方法写出一个代数恒等式是( )
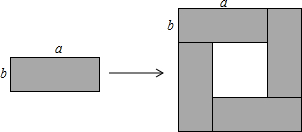

| A. | a2+2ab+b2=(a+b)2 | B. | a2-2ab+b2=(a-b)2 | C. | (a+b)(a-b)=a2-b2 | D. | 4ab=(a+b)2-(a-b)2 |