题目内容
8.设直线nx+(n+1)y=$\sqrt{2}$(n为自然数)与两坐标轴围成的三角形面积为Sn,则S1+S2+…+S2016的值为$\frac{2016}{2017}$.分析 先利用坐标轴上点的坐标特征求出直线与x轴和y轴的坐标,则利用三角形面积公式得到Sn=$\frac{1}{n(n+1)}$,再分别计算出S1,S2,S3,S2015,然后利用$\frac{1}{n(n+1)}$=$\frac{1}{n}$-$\frac{1}{n+1}$求它们的和.
解答 解:当x=0时,y=$\frac{\sqrt{2}}{n+1}$,则直线与y轴的交点坐标为(0,$\frac{\sqrt{2}}{n+1}$),
当y=0时,x=$\frac{\sqrt{2}}{n}$,则直线与x轴的交点坐标为($\frac{\sqrt{2}}{n}$,0),
所以Sn=$\frac{1}{2}$•$\frac{\sqrt{2}}{n}$•$\frac{\sqrt{2}}{n+1}$=$\frac{1}{n(n+1)}$,
当n=1时,S1=$\frac{1}{1×2}$,
当n=2时,S2=$\frac{1}{2×3}$,
当n=3时,S3=$\frac{1}{3×4}$,
…
当n=2016时,S2016=$\frac{1}{2016×2017}$,
所以S1+S2+S3+…+S2015=$\frac{1}{1×2}$+$\frac{1}{2×3}$+$\frac{1}{3×4}$+…+$\frac{1}{2016×2017}$=1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{4}$+…+$\frac{1}{2016}$-$\frac{1}{2017}$=1-$\frac{1}{2017}$=$\frac{2016}{2017}$.
点评 本题考查了一次函数图象上点的坐标特征:一次函数图象上点的坐标满足其解析式,解决此类问题时求出直线与坐标轴的交点坐标.熟练运用$\frac{1}{n(n+1)}$=$\frac{1}{n}$-$\frac{1}{n+1}$是解决此题的关键.

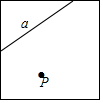
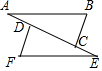 如图,已知,∠A=∠E,AD=EC,若要△ABC≌△EFD,则可添加下列条件的是( )
如图,已知,∠A=∠E,AD=EC,若要△ABC≌△EFD,则可添加下列条件的是( )| A. | AB=EF | B. | AC=ED | C. | BC=DF | D. | ∠B=∠BDF |
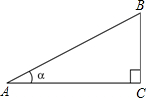 如图,定义:在直角三角形ABC中,锐角α的邻边与对边的比叫做角α的余切,记作ctanα,即ctanα=$\frac{角α的邻边}{角α的对边}$=$\frac{AC}{BC}$,根据上述角的余切定义,解下列问题:
如图,定义:在直角三角形ABC中,锐角α的邻边与对边的比叫做角α的余切,记作ctanα,即ctanα=$\frac{角α的邻边}{角α的对边}$=$\frac{AC}{BC}$,根据上述角的余切定义,解下列问题:
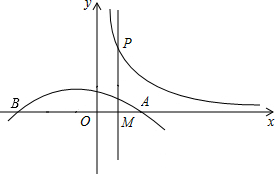 如图,抛物线L:y=-$\frac{1}{2}$(x-1)(x+3)与x轴从左到右的交点为B,A,过线段OA的中点M作MP⊥x轴,交双曲线y=$\frac{k}{x}$(k>0,x>0)于点P,且OA•MP=8.
如图,抛物线L:y=-$\frac{1}{2}$(x-1)(x+3)与x轴从左到右的交点为B,A,过线段OA的中点M作MP⊥x轴,交双曲线y=$\frac{k}{x}$(k>0,x>0)于点P,且OA•MP=8.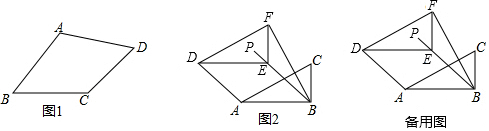
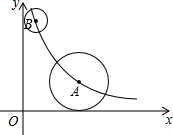 如图,在平面直角坐标系中,点A、B均在函数y=$\frac{k}{x}$(k>0,x>0)的图象上,⊙A与x轴相切,⊙B与y轴相切.若点A的坐标为(3,2),且⊙A的半径是⊙B的半径的2倍,则点B的坐标为(1,6).
如图,在平面直角坐标系中,点A、B均在函数y=$\frac{k}{x}$(k>0,x>0)的图象上,⊙A与x轴相切,⊙B与y轴相切.若点A的坐标为(3,2),且⊙A的半径是⊙B的半径的2倍,则点B的坐标为(1,6).