题目内容
3.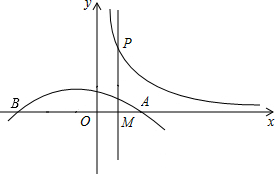 如图,抛物线L:y=-$\frac{1}{2}$(x-1)(x+3)与x轴从左到右的交点为B,A,过线段OA的中点M作MP⊥x轴,交双曲线y=$\frac{k}{x}$(k>0,x>0)于点P,且OA•MP=8.
如图,抛物线L:y=-$\frac{1}{2}$(x-1)(x+3)与x轴从左到右的交点为B,A,过线段OA的中点M作MP⊥x轴,交双曲线y=$\frac{k}{x}$(k>0,x>0)于点P,且OA•MP=8.(1)求k的值;
(2)求AB长;
(3)求抛物线L的对称轴与顶点坐标,并求直线MP与L对称轴之间的距离;
(4)当抛物线向右平移3个单位后,其顶点是否落在双曲线上,说明理由.
分析 (1)先根据点M是OA中点得出OM=$\frac{1}{2}$OA,进而由OA•MP=8,得出OM•MP=4即可得出结论;
(2)令y=0直接求出点A,B坐标即可求出AB;
(3)先确定出抛物线的对称轴为x=-1,再求出点M的坐标即可得出结论;
(4)先确定出平移后的抛物线的顶点坐标代入双曲线解析式中判断即可.
解答 解:(1)设P(x,y)
∵M是线段OA的中点,
∴OM=$\frac{1}{2}$OA,
∵OA•MP=8,
∴OM•MP=4,
∴xy=4,
∵点P在双曲线上,
∴k=xy=4;
(2)令y=0,则0=-$\frac{1}{2}$(x-1)(x+3),
∴x=1或x=-3,
∴B(-3,0),A(1,0),
∴AB=4;
(3)由(2)知,B(-3,0),A(1,0),
∴抛物线的对称轴为x=-1,
当x=-1时,y=2,
∴抛物线的顶点坐标为(-1,2),
∵M是OA的中点,A(1,0),
∴M($\frac{1}{2}$,0),抛物线的对称轴为x=-1,
∴直线MP与L对称轴之间的距离为$\frac{3}{2}$;
(4)在双曲线上,
理由:∵抛物线的顶点坐标为(-1,2),
当抛物线向右平移3个单位后,其顶点坐标为(2,2),
把(2,2)代入双曲线的解析式为y=$\frac{4}{x}$中,得出,左边=右边,
∴(2,2)在双曲线上.
即:平移后抛物线的顶点落在双曲线上.
点评 此题是二次函数综合题,主要考查了待定系数法,抛物线与x轴的交点坐标的确定,抛物线顶点坐标的确定,解(1)的关键是得出OM=$\frac{1}{2}$OA,解(2)的关键是确定出点A,B坐标,解(3)的关键是确定出M的坐标,解(4)的关键是确定出平移后抛物线的顶点坐标.

练习册系列答案
 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
12.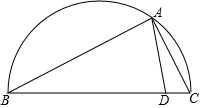 如图,以BC为直径的半圆中,A为弧BC上一点,AC=$\sqrt{3}$,AB=4,D为BC上一点,∠CAD=30°,则AD的长为( )
如图,以BC为直径的半圆中,A为弧BC上一点,AC=$\sqrt{3}$,AB=4,D为BC上一点,∠CAD=30°,则AD的长为( )
 如图,以BC为直径的半圆中,A为弧BC上一点,AC=$\sqrt{3}$,AB=4,D为BC上一点,∠CAD=30°,则AD的长为( )
如图,以BC为直径的半圆中,A为弧BC上一点,AC=$\sqrt{3}$,AB=4,D为BC上一点,∠CAD=30°,则AD的长为( )| A. | $\frac{9}{5}$ | B. | $\frac{8}{5}$ | C. | $\frac{7}{5}$ | D. | $\frac{6}{5}$ |
13.下列运算正确的是( )
| A. | x3+x3=2x6 | B. | (x2)3=x5 | C. | x6÷x2=x3 | D. | x2•x3=x5 |
 如图,四边形ABCD中,∠ADC的角平分线DE与∠BCD的角平分线CA相交于E点,DE交BC于点F,连结AF,已知∠ACD=32°,∠CDE=58°.
如图,四边形ABCD中,∠ADC的角平分线DE与∠BCD的角平分线CA相交于E点,DE交BC于点F,连结AF,已知∠ACD=32°,∠CDE=58°. 请根据图编写一道题,并给出解答.
请根据图编写一道题,并给出解答.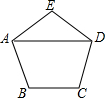 如图所示,正五边形ABCDE的边长为10cm,则对角线AD=5+5$\sqrt{5}$cm.
如图所示,正五边形ABCDE的边长为10cm,则对角线AD=5+5$\sqrt{5}$cm.