题目内容
18.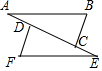 如图,已知,∠A=∠E,AD=EC,若要△ABC≌△EFD,则可添加下列条件的是( )
如图,已知,∠A=∠E,AD=EC,若要△ABC≌△EFD,则可添加下列条件的是( )| A. | AB=EF | B. | AC=ED | C. | BC=DF | D. | ∠B=∠BDF |
分析 根据全等三角形的判定定理逐个判断即可.
解答 解:∵AD=CE,
∴AD+DC=CE+DC,
∴AC=DE,
A、AB=EF、∠A=∠E、AC=ED,符合全等三角形的判定定理SAS,能推出△ABC≌△EFD,故本选项符合题意;
B、∠A=∠E和AC=ED,不符合全等三角形的判定定理,不能推出△ABC≌△EFD,故本选项不符合题意;
C、BC=DF,AC=DE、∠A=∠E,不符合全等三角形的判定定理HL,能推出△ABC≌△EFD,故本选项不符合题意;
D、∠A=∠E、∠B=∠BDF、AC=DE,不符合全等三角形的判定定理,不能推出△ABC≌△EFD,故本选项不符合题意;
故选A.
点评 本题考查了全等三角形的判定定理,能熟记判定定理的内容是解此题的关键,注意:全等三角形的判定定理有SAS,ASA,AAS,SSS,直角三角形全等还有HL.

练习册系列答案
相关题目
6.在0,-2,-1,$\frac{1}{2}$这四个数中,最小的数是( )
| A. | 0 | B. | -2 | C. | -1 | D. | $\frac{1}{2}$ |
13.下列运算正确的是( )
| A. | x3+x3=2x6 | B. | (x2)3=x5 | C. | x6÷x2=x3 | D. | x2•x3=x5 |
3.下列运算正确的是( )
| A. | a3•a3=2a3 | B. | a0÷a3=a-3 | C. | (ab2)3=ab6 | D. | (a3)2=a5 |
10.已知点P(a,2),Q(-1,b)关于x轴对称,则点(a,b)位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
7.如图,等腰Rt△ABC中,∠ACB=90°,AC=BC=1,且AC边在直线a上,将△ABC绕点A瞬时针旋转到位置①可得到点P1,此时AP1=$\sqrt{2}$;将位置①的三角形绕点P1顺时针旋转到位置②,可得到点P2,此时AP2=$\sqrt{2}$+1;将位置②的三角形绕点P2顺时针旋转到位置③,可得到点P3,此时AP3=$\sqrt{2}$+2;…,按此规律继续旋转,直至得到点P2017为止,则AP2017长为( )


| A. | 1344+672$\sqrt{2}$ | B. | 1344+673$\sqrt{2}$ | C. | 1345+673$\sqrt{2}$ | D. | 1345+674$\sqrt{2}$ |