题目内容
20.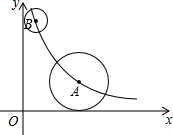 如图,在平面直角坐标系中,点A、B均在函数y=$\frac{k}{x}$(k>0,x>0)的图象上,⊙A与x轴相切,⊙B与y轴相切.若点A的坐标为(3,2),且⊙A的半径是⊙B的半径的2倍,则点B的坐标为(1,6).
如图,在平面直角坐标系中,点A、B均在函数y=$\frac{k}{x}$(k>0,x>0)的图象上,⊙A与x轴相切,⊙B与y轴相切.若点A的坐标为(3,2),且⊙A的半径是⊙B的半径的2倍,则点B的坐标为(1,6).
分析 由点A的坐标利用反比例函数图象上点的坐标特征即可求出k值,根据切线的性质结合两圆半径间的关系即可得出点B的横坐标,再根据反比例函数图象上点的坐标特征即可求出点B的坐标.
解答 解:∵点A(3,2)在函数y=$\frac{k}{x}$(k>0,x>0)的图象上,
∴k=3×2=6.
∵⊙A与x轴相切,⊙B与y轴相切,点A的坐标为(3,2),且⊙A的半径是⊙B的半径的2倍,
∴点B的横坐标为1.
∵点B在反比例函数y=$\frac{6}{x}$的图象上,
∴点B的坐标为(1,6).
故答案为:(1,6).
点评 本题考查了反比例函数图象上点的坐标特征以及切线的性质,根据点B的坐标利用反比例函数图象上点的坐标特征求出k值是解题的关键.

练习册系列答案
相关题目
12.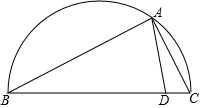 如图,以BC为直径的半圆中,A为弧BC上一点,AC=$\sqrt{3}$,AB=4,D为BC上一点,∠CAD=30°,则AD的长为( )
如图,以BC为直径的半圆中,A为弧BC上一点,AC=$\sqrt{3}$,AB=4,D为BC上一点,∠CAD=30°,则AD的长为( )
 如图,以BC为直径的半圆中,A为弧BC上一点,AC=$\sqrt{3}$,AB=4,D为BC上一点,∠CAD=30°,则AD的长为( )
如图,以BC为直径的半圆中,A为弧BC上一点,AC=$\sqrt{3}$,AB=4,D为BC上一点,∠CAD=30°,则AD的长为( )| A. | $\frac{9}{5}$ | B. | $\frac{8}{5}$ | C. | $\frac{7}{5}$ | D. | $\frac{6}{5}$ |
10.已知点P(a,2),Q(-1,b)关于x轴对称,则点(a,b)位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
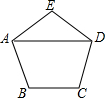 如图所示,正五边形ABCDE的边长为10cm,则对角线AD=5+5$\sqrt{5}$cm.
如图所示,正五边形ABCDE的边长为10cm,则对角线AD=5+5$\sqrt{5}$cm.