题目内容
3. 如图,一船在某灯墙C正东方向10海里处的A点,以25海里/时的速度沿北偏西30°方向航行.
如图,一船在某灯墙C正东方向10海里处的A点,以25海里/时的速度沿北偏西30°方向航行.(1)问多长时间后,船距灯塔最近?
(2)求船到达灯塔的正北方向时航行了多少海里?此时,距离灯塔有多远?(结果保留根号)
分析 (1)过C作CD⊥AB于D,根据垂线段最近,则CD最小,由三角函数求得CD,再由速度公式求得结论;
(2)根据已知条件利用三角函数即可求得BC,AB的长.
解答 解:(1)过C作CD⊥AB于D,则CD最小,
由题意知∠BAC=90°-30°=60°,
∴AD=$\frac{1}{2}$AC=5(海里),5÷25=0.1(小时),
故0.1小时后,船距灯塔最近;
(2)在直角△ABC中,∠BAC=60°,AC=10海里,tan∠BAC=$\frac{BC}{AC}$,
所以BC=AC•tan60°=10$\sqrt{3}$海里,AB=2AC=20海里,
答:船到达灯塔的正北方向时航行了20海里,此时,距离灯塔有10$\sqrt{3}$海里.
点评 本题主要考查了方向角含义,三角函数,解直角三角形的应用,正确记忆三角函数的定义是解决本题的关键.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
15. 某物体的三视图如图,那么该物体形状可能是( )
某物体的三视图如图,那么该物体形状可能是( )
 某物体的三视图如图,那么该物体形状可能是( )
某物体的三视图如图,那么该物体形状可能是( )| A. | 长方体 | B. | 圆锥 | C. | 正方体 | D. | 圆柱 |
13. 如图是某个几何体的三视图,该几何体是( )
如图是某个几何体的三视图,该几何体是( )
 如图是某个几何体的三视图,该几何体是( )
如图是某个几何体的三视图,该几何体是( )| A. | 三棱柱 | B. | 三棱锥 | C. | 圆锥 | D. | 圆柱 |
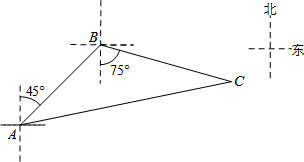 如图,禁止捕鱼期间,某海上稽查队在某海域巡逻,上午某一时刻在A处接到指挥部通知,在他们东北方向距离12海里的B处有一艘捕鱼船,正在沿南偏东75°方向航行,稽查队员立即乘坐巡逻船以每小时14海里的速度沿北偏东某一方向出发行驶了2小时,在C处成功拦截捕鱼船,求捕鱼船的速度.
如图,禁止捕鱼期间,某海上稽查队在某海域巡逻,上午某一时刻在A处接到指挥部通知,在他们东北方向距离12海里的B处有一艘捕鱼船,正在沿南偏东75°方向航行,稽查队员立即乘坐巡逻船以每小时14海里的速度沿北偏东某一方向出发行驶了2小时,在C处成功拦截捕鱼船,求捕鱼船的速度.

 尺规作图:如图,线段AB,BC,∠ABC=90°.求作:矩形ABCD.小明的作图过程如下:
尺规作图:如图,线段AB,BC,∠ABC=90°.求作:矩形ABCD.小明的作图过程如下: 如图,货轮在海上以30海里/时的速度匀速航行,为了确定船位,当货轮在B点时,观察灯塔A在其南偏东60°方向上,货轮沿南偏东30°方向航行半小时到达C点,观察灯塔A在其北偏东75°方向上,求此时货轮距离灯塔A的距离(即AC的长)(结果保留一位小数,参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)
如图,货轮在海上以30海里/时的速度匀速航行,为了确定船位,当货轮在B点时,观察灯塔A在其南偏东60°方向上,货轮沿南偏东30°方向航行半小时到达C点,观察灯塔A在其北偏东75°方向上,求此时货轮距离灯塔A的距离(即AC的长)(结果保留一位小数,参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)