题目内容
11.在等边△ABC中,点D是线段BC的中点,∠EDF=120?,射线DE与线段AB相交于点E.射线DF与线段AC(或AC的延长线)相交于点F.(1)如图1,若DF⊥AC,请直接写出DE与AB的位置关系;
(2)如图2,将(1)中的∠EDF绕点D顺时针旋转一定的角度,DF仍与线段AC相交于点F.求证:DE=DF;
(3)在∠EDF绕点D顺时针旋转过程中,直接用等式表示线段BE、CF、AB之间的数量关系.
(4)当∠EDF绕点D顺时针旋转到如图3位置时,DF与线段AC的延长线相交于点F,若DN⊥AC于点N,若DN=FN,AB=10,直接写出BE+CF的值.

分析 (1)根据四边形的内角和即可得到结论;
(2)连接AD,过点D作DM⊥AB于M,作DN⊥AC于N,如图2,由点D是线段BC的中点,得到AD是∠BAC的角平分线,根据角平分线的性质得到DM=DN,根据全等三角形的性质即可得到结论;
(3)如图2(a)中,过点D作DM⊥AB于M,作DN⊥AC于N.根据全等三角形的性质得到BM=CN,DM=DN,ME=NF,于是得到结论;
(4)过点D作DM⊥AB于M,如图2(b),由(3)可得:BM=CN,DM=DN,EM=FN.根据已知条件得到DM=DN=FN=EM,于是得到结论.
解答 解:(1)∵DF⊥AC,
∴∠AFD=90°,
∵∠A=60°,∠EDF=120?,
∴∠AED=360°-∠A-∠AFD-∠EDF=90°,
∴DE⊥AB;
(2)连接AD,过点D作DM⊥AB于M,作DN⊥AC于N,如图2,
∵点D是线段BC的中点,
∴AD是∠BAC的角平分线,
∴DM=DN,
∵∠AMD=∠BMD=∠AND=∠CND=90°
∵∠A=60°,
∴∠MDN=360°-60°-90°-90°=120°.
∵∠EDF=120°,
∴∠MDE=∠NDF,
在△EMD和△FND中,
$\left\{\begin{array}{l}{∠EMD=∠FND}\\{DM=DN}\\{∠MDE=∠NDF}\end{array}\right.$,
∴△EMD≌△FND,
∴DE=DF;
(3)如图2(a)中,过点D作DM⊥AB于M,作DN⊥AC于N.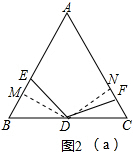
在△BDM与△CDN中,$\left\{\begin{array}{l}{∠B=∠C=60°}\\{∠BMD=∠DNC=90°}\\{BD=CD}\end{array}\right.$,
∴△BDM≌△CDN,
∴BM=CN,DM=DN,
又∵∠EDF=120°=∠MDN,
∴∠EDM=∠NDF,
在△DME与△DNF中,$\left\{\begin{array}{l}{∠EDM=∠FDN}\\{∠DME=∠DNF}\\{DM=DN}\end{array}\right.$,
∴△EDM≌△FDN,
∴ME=NF,
∴BE+CF=BM+EM+NC-FN=2BM=BD=$\frac{1}{2}$AB;
如图3,同理BM=CN,DM=DN,
又∵∠EDF=120°=∠MDN,
∴∠EDM=∠NDF,
又∵∠EMD=∠FND=90°,
∴△EDM≌△FDN,
∴ME=NF,
∴BE-CF=BM+EM-(FN-CN)=2BM=BD=$\frac{1}{2}$AB,
综上所述,线段BE、CF、AB之间的数量关系为:BE+CF=$\frac{1}{2}$AB或BE-CF=$\frac{1}{2}$AB;
(4)过点D作DM⊥AB于M,如图2(b),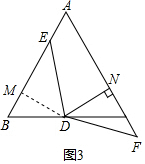
∵∠B=∠ACD=60°.
由(3)可得:BM=CN,DM=DN,EM=FN.
∵DN=FN,
∴DM=DN=FN=EM,
∴BE+CF=BM+EM+CF=CN+DM+CF=NF+DM=2DM=2BD×sin60°=$\frac{\sqrt{3}}{2}$BC=$\frac{\sqrt{3}}{2}$AB,
∵AB=10,
∴BE+CF=5$\sqrt{3}$.
点评 本题主要考查了等边三角形的判定与性质、四边形的内角和定理、全等三角形的判定与性质、三角函数的定义、特殊角的三角函数值等知识,通过证明三角形全等得到BM=CN,DM=DN,EM=FN是解决本题的关键.

| A. | 1尾 | B. | 50尾 | C. | 500尾 | D. | 1 000尾 |
| 组别 | 正确字数x | 人数 |
| A | 0≤x<8 | 10 |
| B | 8≤x<16 | 15 |
| C | 16≤x<24 | 25 |
| D | 24≤x<32 | m |
| E | 32≤x<40 | n |

根据以上信息解决下列问题:
(1)在统计表中,m=30,n=20,并补全条形统计图.
(2)扇形统计图中“C组”所对应的圆心角的度数是90°.
(3)若该校共有1120名学生,如果听写正确的个数少于24个定为不合格,请你估计这所学校本次比赛听写不合格的学生人数.
| 编号 | 教学方式 | 最喜欢的频数 | 频率 |
| 1 | 教师讲,学生听 | 20 | 0.10 |
| 2 | 教师提出问题,学生探索思考 | ||
| 3 | 学生自行阅读教材,独立思考 | 30 | |
| 4 | 分组讨论,解决问题 | 0.25 |

(1)收回的问卷份数为200,把条形统计图补充完整;
(2)扇形统计图中编号1与编号4的圆心角分别是多少度?
(3)你最喜欢以上哪一种教学方式,请提出你的建议,并简要说明理由.
 如图,某人为了测量小山顶上的塔ED的高,他在山下的点A处测得塔尖点D的仰角为45°,再沿AC方向前进60m到达山脚点B,测得塔尖点D的仰角为60°,塔底点E的仰角为30°,求塔ED的高度.(结果保留根号)
如图,某人为了测量小山顶上的塔ED的高,他在山下的点A处测得塔尖点D的仰角为45°,再沿AC方向前进60m到达山脚点B,测得塔尖点D的仰角为60°,塔底点E的仰角为30°,求塔ED的高度.(结果保留根号)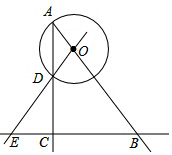 如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,O是射线AB上的一个动点,以点O为圆心,OA为半径的⊙O与射线AC的另一个交点为D,直线OD交直线BC于点E.
如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,O是射线AB上的一个动点,以点O为圆心,OA为半径的⊙O与射线AC的另一个交点为D,直线OD交直线BC于点E. 如图,一船在某灯墙C正东方向10海里处的A点,以25海里/时的速度沿北偏西30°方向航行.
如图,一船在某灯墙C正东方向10海里处的A点,以25海里/时的速度沿北偏西30°方向航行.
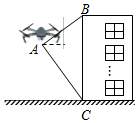 台州湾循环经济产业集聚区正在投资建设无人机小镇,无人机已运用于很多行业.一测绘无人机从A处测得某建筑物顶部B的仰角为37°,底部C的俯角为60°,此时无人机与建筑物水平距离为30米,建筑物的高度BC约为多少米?
台州湾循环经济产业集聚区正在投资建设无人机小镇,无人机已运用于很多行业.一测绘无人机从A处测得某建筑物顶部B的仰角为37°,底部C的俯角为60°,此时无人机与建筑物水平距离为30米,建筑物的高度BC约为多少米?