题目内容
12. 如图,货轮在海上以30海里/时的速度匀速航行,为了确定船位,当货轮在B点时,观察灯塔A在其南偏东60°方向上,货轮沿南偏东30°方向航行半小时到达C点,观察灯塔A在其北偏东75°方向上,求此时货轮距离灯塔A的距离(即AC的长)(结果保留一位小数,参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)
如图,货轮在海上以30海里/时的速度匀速航行,为了确定船位,当货轮在B点时,观察灯塔A在其南偏东60°方向上,货轮沿南偏东30°方向航行半小时到达C点,观察灯塔A在其北偏东75°方向上,求此时货轮距离灯塔A的距离(即AC的长)(结果保留一位小数,参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)
分析 过C作CD⊥AB于D,解直角三角形即可得到结论.
解答  解:过C作CD⊥AB于D,由题意得,∠ABC=30°,∠BCF=30°,
解:过C作CD⊥AB于D,由题意得,∠ABC=30°,∠BCF=30°,
∵∠ACF=75°,
∴∠ACB=105°,
∴∠BCD=60°,∠ACD=45°,
在Rt△BCD中,BC=30×0.5=15海里,
∵cos∠ABC=$\frac{CD}{AC}$,
∴AC=$\frac{CD}{cos45°}$=7.5×1,41=10.6海里,
答:货轮距离灯塔A的距离是10.6海里.
点评 本题考查了等腰直角三角形和方向角,根据方向角求出三角形各角的度数是解题的关键.

练习册系列答案
相关题目
2.一池塘中大约有鱼苗数为50 000尾,为了解池塘中鱼苗的长势,现需从中捞取一些鱼苗进行抽样调查,那么捞出鱼苗数最合适的是( )
| A. | 1尾 | B. | 50尾 | C. | 500尾 | D. | 1 000尾 |
 如图,一船在某灯墙C正东方向10海里处的A点,以25海里/时的速度沿北偏西30°方向航行.
如图,一船在某灯墙C正东方向10海里处的A点,以25海里/时的速度沿北偏西30°方向航行.
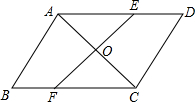 如图,四边形ABCD中,AD∥BC,∠B=∠D,点E、F分别在AD、BC上,EF与AC相交于点O.
如图,四边形ABCD中,AD∥BC,∠B=∠D,点E、F分别在AD、BC上,EF与AC相交于点O.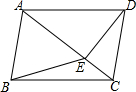 如图,在四边形ABCD中,AB∥CD,∠ABC=∠ADC,DE垂直于对角线AC,垂足是E,连接BE.
如图,在四边形ABCD中,AB∥CD,∠ABC=∠ADC,DE垂直于对角线AC,垂足是E,连接BE.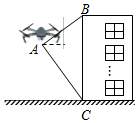 台州湾循环经济产业集聚区正在投资建设无人机小镇,无人机已运用于很多行业.一测绘无人机从A处测得某建筑物顶部B的仰角为37°,底部C的俯角为60°,此时无人机与建筑物水平距离为30米,建筑物的高度BC约为多少米?
台州湾循环经济产业集聚区正在投资建设无人机小镇,无人机已运用于很多行业.一测绘无人机从A处测得某建筑物顶部B的仰角为37°,底部C的俯角为60°,此时无人机与建筑物水平距离为30米,建筑物的高度BC约为多少米? 将边长为2的等边△OAB按如图位置放置,AB边与y轴的交点为C,则OC=$3\sqrt{2}-\sqrt{6}$.
将边长为2的等边△OAB按如图位置放置,AB边与y轴的交点为C,则OC=$3\sqrt{2}-\sqrt{6}$.